题目内容
8.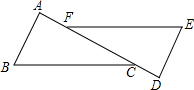 如图,已知A,F,C在一条直线上,且AF=DC,AB∥DE,EF∥CB,求证:BC=EF.
如图,已知A,F,C在一条直线上,且AF=DC,AB∥DE,EF∥CB,求证:BC=EF.
分析 利用AF=DC求出AC=DF,根据AB∥DE,EF∥CB,求出∠A=∠D,∠BCA=∠EFD,根据ASA证出△ABC≌△DEF,推出BC=EF即可.
解答 证明:∵AF=CD,
∴AF+CF=CD+CF,
即AC=DF,
∵AB∥DE,EF∥CB,
∴∠A=∠D,∠BCA=∠EFD,
在△ABC和△DEF中
$\left\{\begin{array}{l}{∠A=∠D}\\{AC=DF}\\{∠BCA=∠EFD}\end{array}\right.$,
∴△ABC≌△DEF,
∴BC=EF.
点评 本题考查了等式性质,全等三角形的性质和判定,平行线的性质和判定等知识点的运用,关键是推出△ABC≌△DEF,培养了学生运用定理进行推理的能力.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
18.一个三角形的三边长分别为x、2、3,那么x的取值范围是( )
| A. | 2<x<3 | B. | 1<x<5 | C. | 2<x<5 | D. | x>2 |
19.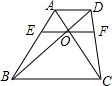 如图,在梯形ABCD中,AD∥BC,AC,BD相交于点O,过点O作EF∥AD分别交AB,CD于点E、F.下列各式中不正确的是( )
如图,在梯形ABCD中,AD∥BC,AC,BD相交于点O,过点O作EF∥AD分别交AB,CD于点E、F.下列各式中不正确的是( )
 如图,在梯形ABCD中,AD∥BC,AC,BD相交于点O,过点O作EF∥AD分别交AB,CD于点E、F.下列各式中不正确的是( )
如图,在梯形ABCD中,AD∥BC,AC,BD相交于点O,过点O作EF∥AD分别交AB,CD于点E、F.下列各式中不正确的是( )| A. | $\frac{AE}{EB}$=$\frac{DF}{FC}$ | B. | $\frac{OA}{OC}$=$\frac{OD}{OB}$ | C. | $\frac{AE}{AB}$=$\frac{DO}{BO}$ | D. | $\frac{CD}{CF}$=$\frac{BD}{BO}$ |
 已知:如图,在Rt△ABC中,∠ACB=90°,CD是中线,CE是高,且AC2=3BC2.求证:CD、CE三等分∠ACB.
已知:如图,在Rt△ABC中,∠ACB=90°,CD是中线,CE是高,且AC2=3BC2.求证:CD、CE三等分∠ACB.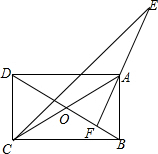 如图,已知矩形ABCD中,AC,BD交于点O,AF⊥BD垂足为F,∠BCD的平分线交FA的延长线于点E,求证:AC=AE.
如图,已知矩形ABCD中,AC,BD交于点O,AF⊥BD垂足为F,∠BCD的平分线交FA的延长线于点E,求证:AC=AE.