题目内容
2.应用向量法证明三角形中位线定理.分析 首先根据题意画出图形,根据图形写出已知、求证;然后利用三角形法则,分别表示出$\overrightarrow{DE}$,$\overrightarrow{BC}$,则可得$\overrightarrow{DE}$=$\frac{1}{2}$$\overrightarrow{BC}$,继而证得结论.
解答 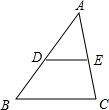 已知:如图,点D,E分别是AB,AC的中点,
已知:如图,点D,E分别是AB,AC的中点,
求证:DE∥BC,DE=$\frac{1}{2}$BC.
证明:∵点D,E分别是AB,AC的中点,
∴$\overrightarrow{DA}$=$\frac{1}{2}$$\overrightarrow{BA}$,$\overrightarrow{AE}$=$\frac{1}{2}$$\overrightarrow{AC}$,
∴$\overrightarrow{DE}$=$\overrightarrow{DA}$+$\overrightarrow{AE}$=$\frac{1}{2}$$\overrightarrow{BA}$+$\frac{1}{2}$$\overrightarrow{AC}$=$\frac{1}{2}$($\overrightarrow{BA}$+$\overrightarrow{AC}$),$\overrightarrow{BC}$=$\overrightarrow{BA}$+$\overrightarrow{AC}$,
∴$\overrightarrow{DE}$=$\frac{1}{2}$$\overrightarrow{BC}$,
∴DE∥BC,DE=$\frac{1}{2}$BC.
点评 此题考查了平面向量的知识.注意利用三角形法则证得$\overrightarrow{DE}$=$\frac{1}{2}$$\overrightarrow{BC}$是解此题的关键.

| A. | $\left\{\begin{array}{l}x+y=12\\ 2x+y=20\end{array}\right.$ | B. | $\left\{\begin{array}{l}x+y=12\\ x+2y=20\end{array}\right.$ | C. | $\left\{\begin{array}{l}x+y=20\\ x+2y=12\end{array}\right.$ | D. | $\left\{\begin{array}{l}x+y=20\\ 2x+y=12\end{array}\right.$ |
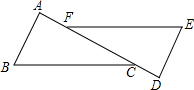 如图,已知A,F,C在一条直线上,且AF=DC,AB∥DE,EF∥CB,求证:BC=EF.
如图,已知A,F,C在一条直线上,且AF=DC,AB∥DE,EF∥CB,求证:BC=EF.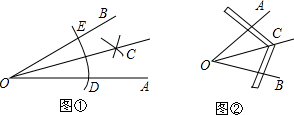
 如图,P为矩形ABCD外一点,猜想S△PBC、S△PAC、S△PCD之间的数量关系,并证明.
如图,P为矩形ABCD外一点,猜想S△PBC、S△PAC、S△PCD之间的数量关系,并证明.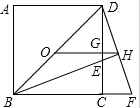 已知:如图,正方形ABCD中,O是BD的中点,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连接DF,交BE的延长线于点G,连接OG.
已知:如图,正方形ABCD中,O是BD的中点,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连接DF,交BE的延长线于点G,连接OG.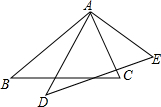 如图,已知△ABC≌△ADE,D是∠BAC的平分线上一点,且∠BAC=70°,则∠CAE=35度.
如图,已知△ABC≌△ADE,D是∠BAC的平分线上一点,且∠BAC=70°,则∠CAE=35度.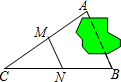 A、B两点被池塘隔开(如图),在AB外选一点C,连结AC和BC并分别找出其中点M、N,若测得MN=100m,则A、B两点的距离为200m.
A、B两点被池塘隔开(如图),在AB外选一点C,连结AC和BC并分别找出其中点M、N,若测得MN=100m,则A、B两点的距离为200m.