题目内容
4.已知方程组$\left\{\begin{array}{l}{x-y=3a+6}\\{x+y=-a-12}\end{array}\right.$的解满足y<x≤0.(1)求a的取值范围;
(2)化简|a-3|+|a+1|.
分析 (1)把a看做已知数求出方程组的解得到x与y,代入不等式求出a的范围即可;
(2)根据a的范围,利用绝对值的代数意义求出原式的值即可.
解答 解:(1)$\left\{\begin{array}{l}{x-y=3a+6①}\\{x+y=-a-12②}\end{array}\right.$,
①+②得:2x=2a-6,即x=a-3③,
把③代入②得:a-3+y=-a-12,即y=-2a-9,
代入不等式得:-2a-9<a-3≤0,
解得:-2<a≤3;
(2)当-2<a≤3,∴a-3≤0,
当-1≤a≤3时,可得a+1≥0,原式=3-a+a+1=4;
当-2<a<-1时,可得a+1<0,原式=3-a-a-1=-2a+2.
点评 此题考查了二元一次方程组的解,以及解一元一次不等式组,熟练掌握运算法则是解本题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
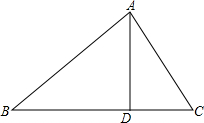 有一块三角形铁皮ABC,已知最长边BC=12,高AD=8,要把它加工成一个矩形铁皮,使矩形的一边在BC上,其余两个顶点分别在AB,AC上,问:加工成的矩形铁皮的面积最大值是多少平方厘米?
有一块三角形铁皮ABC,已知最长边BC=12,高AD=8,要把它加工成一个矩形铁皮,使矩形的一边在BC上,其余两个顶点分别在AB,AC上,问:加工成的矩形铁皮的面积最大值是多少平方厘米?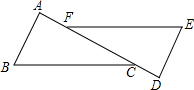 如图,已知A,F,C在一条直线上,且AF=DC,AB∥DE,EF∥CB,求证:BC=EF.
如图,已知A,F,C在一条直线上,且AF=DC,AB∥DE,EF∥CB,求证:BC=EF.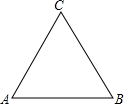 已知等边△ABC,请做出旋转后的三角形.
已知等边△ABC,请做出旋转后的三角形.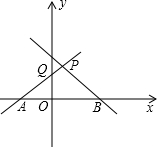 如图,直线y=x+n(n>0)交x轴于A,交y轴于Q,直线y=-2x+m(m>n)交x轴于B,交AQ于P.
如图,直线y=x+n(n>0)交x轴于A,交y轴于Q,直线y=-2x+m(m>n)交x轴于B,交AQ于P.
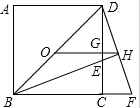 已知:如图,正方形ABCD中,O是BD的中点,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连接DF,交BE的延长线于点G,连接OG.
已知:如图,正方形ABCD中,O是BD的中点,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连接DF,交BE的延长线于点G,连接OG.