题目内容
6.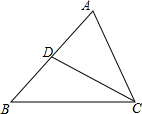 如图,在△ABC中,CD是AB边上的中线,已知∠B=45°,tan∠ACB=2,AC=$\sqrt{5}$,求:
如图,在△ABC中,CD是AB边上的中线,已知∠B=45°,tan∠ACB=2,AC=$\sqrt{5}$,求:(1)△ABC面积;
(2)CD的长;
(3)sin∠ACD的值.
分析 (1)作AH⊥BC于H,设CH=x,则AH=2x,根据勾股定理求出x,从而求出CH和AH,在Rt△ABH中,根据∠B=45°,求出BH=AH=2,再求出BC=BH+CH,最后根据三角形的面积公式进行计算即可;
(2)作DF⊥BC于F,根据DF=$\frac{1}{2}$AH,求出DF,再根据∠B=45°求出BF,从而得出CF的长,最后根据CD=$\sqrt{D{F}^{2}+C{F}^{2}}$代入计算即可;
(3)作DE⊥AC于E,根据S△ACD=$\frac{1}{2}$•AC•DE=$\frac{3}{2}$,求出DE,再根据sin∠ACD=$\frac{DE}{DC}$代入计算即可.
解答 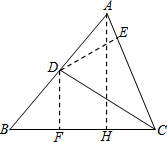 解:(1)作AH⊥BC于H,
解:(1)作AH⊥BC于H,
在Rt△ACH中,
∵tan∠ACB=2,AC=$\sqrt{5}$,
∴$\frac{AH}{CH}$=2,
设CH=x,AH=2x,
根据勾股定理得AC=$\sqrt{5}$x=$\sqrt{5}$,
∴x=1,
∴CH=1,AH=2,
在Rt△ABH中,∠B=45°,
∴BH=AH=2,
∴BC=BH+CH=2+1=3,
∴S△ABC=$\frac{1}{2}$×3×2=3;
(2)作DF⊥BC于F,
∴DF∥AH,
∵BD=AD,
∴DF=$\frac{1}{2}$AH=1,
∴BF=1,
∴CF=3-1=2,
∴CD=$\sqrt{D{F}^{2}+C{F}^{2}}$=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$;
(3)作DE⊥AC于E,
∵S△ACD=$\frac{1}{2}$•AC•DE=$\frac{3}{2}$,
∴$\frac{1}{2}$×$\sqrt{5}$•DE=$\frac{3}{2}$,
∴DE=$\frac{3\sqrt{5}}{5}$,
∴sin∠ACD=$\frac{DE}{DC}$=$\frac{\frac{3\sqrt{5}}{5}}{\sqrt{5}}$=$\frac{3}{5}$.
点评 此题考查勾股定理的运用,三角函数的意义,三角形的面积计算,以及三角形的中位线定理,正确作出两条垂线是解决问题的关键.





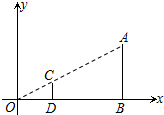 如图,在直角坐标系中,有两点A(6,3)、B(6,0).以原点O为位似中心,相似比为$\frac{1}{3}$,在第一象限内把线段AB缩小后得到线段CD,则点C的坐标为(2,1).
如图,在直角坐标系中,有两点A(6,3)、B(6,0).以原点O为位似中心,相似比为$\frac{1}{3}$,在第一象限内把线段AB缩小后得到线段CD,则点C的坐标为(2,1).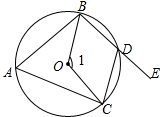 如图所示,已知四边形ABDC是圆内接四边形,∠1=112°,则∠CDE=56度.
如图所示,已知四边形ABDC是圆内接四边形,∠1=112°,则∠CDE=56度. 如图,△ABC中,∠BAC=90°,D是AC上的一点,DE⊥BC于点E,且AD=DE,AE与BD相交于点F.
如图,△ABC中,∠BAC=90°,D是AC上的一点,DE⊥BC于点E,且AD=DE,AE与BD相交于点F. 如图,身高1.6m的小王晚上沿箭头方向散步至一路灯下,他想通过测量自己的影长来估计路灯的高度,具体做法如下:先从路灯底部向东走20步到M处,发观自己的影子端点刚好在两盏路灯的中间点P处,继续沿刚才自己的影子走5步到P处,此时影子的端点在Q处.
如图,身高1.6m的小王晚上沿箭头方向散步至一路灯下,他想通过测量自己的影长来估计路灯的高度,具体做法如下:先从路灯底部向东走20步到M处,发观自己的影子端点刚好在两盏路灯的中间点P处,继续沿刚才自己的影子走5步到P处,此时影子的端点在Q处.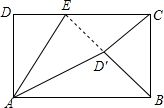 如图,矩形ABCD中,AD=4,AB=7,点E为DC上一动点,△ADE沿AE折叠,点D落在矩形ABCD内一点D′处,若△BCD′为等腰三角形,则DE的长为$\frac{4}{3}$$\sqrt{3}$或$\frac{32-4\sqrt{15}}{7}$.
如图,矩形ABCD中,AD=4,AB=7,点E为DC上一动点,△ADE沿AE折叠,点D落在矩形ABCD内一点D′处,若△BCD′为等腰三角形,则DE的长为$\frac{4}{3}$$\sqrt{3}$或$\frac{32-4\sqrt{15}}{7}$.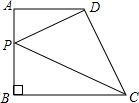 如图,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AD=6,AB=7,BC=8,点P是AB上一个动点.
如图,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AD=6,AB=7,BC=8,点P是AB上一个动点.