题目内容
10.在购买某场足球赛门票时,设购买门票张数为x(张),现有两种购买方案:方案一:若单位赞助广告费10000元,则该单位所购门票的价格为每张60元;(总费用=广告赞助费+门票费)
方案二:购买门票数不超过100张时,每张100元,若超过100元时,超过部分每张80元,
解答下列问题:
(1)方案一种,总费用为10000+60x.方案二中,当0≤x<100时,总费用为100x;当x>100时,总费用为80x+2000.
(2)如果购买本场足球赛门票超过100张,你将选择哪种方案,使总费用最省?请说明理由;
(3)甲,乙两单位分别采用方案一、方案二购买本场足球赛门票共700张,花去总费用计58000元,求甲,乙两单位各购买门票多少张?
分析 (1)依题意可得y与x的函数关系式y=60x+10000;本题考查了分段函数的有关知识(0≤x≤100;x>100);
(2)设60x+10000>80x+2000,可用方案二买;当60x+1000=80x+2000时,两种方案均可选择;当60x+1000<80x+200时,可选择方案一;
(3)设甲、乙单位购买本次足球赛门票数分别为a张、b张,分别可采用方案一或方案二购买.
解答 解:(1)10000+60x;100x; 80x+2000;
故答案为:10000+60x;100x; 80x+2000;
(2)当x>100时,(10000+60x)-(80x+2000)=8000-20x<0,故选取方案二,使总费用最省
(3)设购买方案二的门票x张,买方案一的门票(700-x)张
分两种情况:①当方案二购买的门票数小于100张时,
10000+60(700-x)+100x=58000
解得 x=150>100,不符合题意
②当方案二购买的门票数大于100张时,
10000+60(700-x)+80x+2000=58000
解得 x=200>100,符合题意
则700-200=500张
∴甲乙两单位分别采用方案一、方案二购买本场足球赛门票为500,200张.
点评 (1)利用一次函数求最值时,主要应用一次函数的性质;
(2)用一次函数解决实际问题是近年中考中的热点问题.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
1.下列图形中的曲线不表示y与x的函数的是( )
| A. |  | B. |  | C. |  | D. |  |
18.一次数学活动中,检验两条纸带①、②的边线是否平行,小明和小丽采用两种不同的方法:小明对纸带①沿AB折叠,量得∠1=∠2=50°;小丽对纸带②沿GH折叠,发现GD与GC重合,HF与HE重合.则下列判断正确的是( )
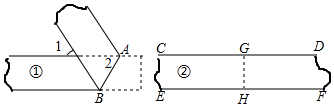

| A. | 纸带①的边线平行,纸带②的边线不平行 | |
| B. | 纸带①的边线不平行,纸带②的边线平行 | |
| C. | 纸带①、②的边线都平行 | |
| D. | 纸带①、②的边线都不平行 |
2.已知A(-$\frac{1}{2}$,y1),B(-1,y2),C($\frac{1}{3}$,y3)是一次函数y=b-$\frac{2}{3}$x图象上三点,则y1,y2,y3的大小关系是( )
| A. | y1<y2<y3 | B. | y3<y1<y2 | C. | y3<y2<y1 | D. | y2<y1<y3 |
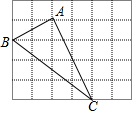 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上.
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上.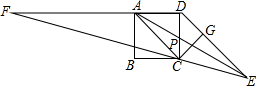 如图,四边形ABCD是正方形,DE∥AC,CE=AC,EC的延长线DA的延长线交于F,连AE交CD于P,作CG⊥DE于G,则下列结论:①AE平分∠CED;②S△ADP=S△EPC;③∠F=∠EAC;④CE=2CG.其中正确的说法有( )
如图,四边形ABCD是正方形,DE∥AC,CE=AC,EC的延长线DA的延长线交于F,连AE交CD于P,作CG⊥DE于G,则下列结论:①AE平分∠CED;②S△ADP=S△EPC;③∠F=∠EAC;④CE=2CG.其中正确的说法有( )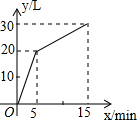 一个装有进水管和出水管的容器,从某时刻开始5min内至进水不出水,在随后的10min内既进水又出水,每分钟的进水量和出水量是两个常数,容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图所示.
一个装有进水管和出水管的容器,从某时刻开始5min内至进水不出水,在随后的10min内既进水又出水,每分钟的进水量和出水量是两个常数,容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图所示.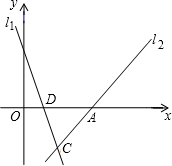 如图,已知直线l1:y=-3x+3与直线l2:y=mx-4m的图象的交点C在第四象限,且点C到y轴的距离为2.
如图,已知直线l1:y=-3x+3与直线l2:y=mx-4m的图象的交点C在第四象限,且点C到y轴的距离为2.