题目内容
15.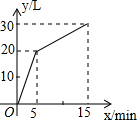 一个装有进水管和出水管的容器,从某时刻开始5min内至进水不出水,在随后的10min内既进水又出水,每分钟的进水量和出水量是两个常数,容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图所示.
一个装有进水管和出水管的容器,从某时刻开始5min内至进水不出水,在随后的10min内既进水又出水,每分钟的进水量和出水量是两个常数,容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图所示.(1)求每分钟进、出水各多少升?
(2)求y与x之间的函数关系式?
(3)第几分钟时容器内的水量为26L?
分析 (1)每分钟的进水量根据前4分钟的图象求出,出水量根据后8分钟的水量变化求解;
(2)用待定系数法求对应的函数关系式即可;
(3)将y=26代入y与x之间的函数关系式得到26=x+15,解方程即可求解.
解答 解:(1)根据图象,每分钟进水20÷5=4(升),
设每分钟出水m升,则 4×10-10m=30-20,
解得:m=3.
故每分钟进水4升、出水3升;
(2)设当0≤x≤5时的直线方程为:y=ax(a≠0).
∵图象过(5,20),
∴5a=20,
解得:a=4,
∴y=4x+15 (0≤x≤5).
设当5≤x≤15时的直线方程为:y=kx+b(k≠0).
∵图象过(5,20)、(15,30),
∴$\left\{\begin{array}{l}{20=5k+b}\\{30=15k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=15}\end{array}\right.$,
∴y=x+15 (5≤x≤12).
故y=$\left\{\begin{array}{l}4x(0≤x≤5)\\ x+15(5≤x≤15)\end{array}\right.$;
(3)当y=26时,即26=x+15,
解得x=11.
故第11分钟时容器内的水量为26L.
点评 此题考查了一次函数的应用,解题时首先正确理解题意,然后根据题意利用待定系数法确定函数的解析式,接着利用函数的性质即可解决问题.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
3. 如图,直线c截两平行直线a,b,则下列式子中一定成立的是( )
如图,直线c截两平行直线a,b,则下列式子中一定成立的是( )
 如图,直线c截两平行直线a,b,则下列式子中一定成立的是( )
如图,直线c截两平行直线a,b,则下列式子中一定成立的是( )| A. | ∠1=∠5 | B. | ∠1=∠4 | C. | ∠2=∠3 | D. | ∠1=∠2 |
5.函数y=$\frac{1}{x-2}$中,x的取值范围是( )
| A. | x≠2 | B. | x>2 | C. | x<2 | D. | x≠-2 |
 有一个“三阶幻方”如图所示,字母A、B、C代表的数字分别是2、8、6.
有一个“三阶幻方”如图所示,字母A、B、C代表的数字分别是2、8、6.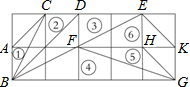 如图所示,在正方形网格上有6个斜三角形,①△ABC,②△BCD,③△BDE,④△BFG,⑤△FGH,⑥△EFK,在②~⑥中,与三角形①相似的有③④⑤(填序号)
如图所示,在正方形网格上有6个斜三角形,①△ABC,②△BCD,③△BDE,④△BFG,⑤△FGH,⑥△EFK,在②~⑥中,与三角形①相似的有③④⑤(填序号)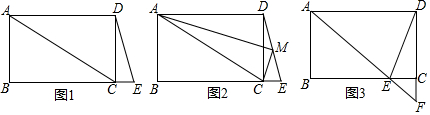
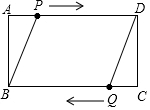 如图,在矩形ABCD中,AB=4cm,AD=6cm,点P从点A出发,以1cm/s的速度沿AD向终点D运动,同时,点Q从点C出发,以1cm/s的速度沿CB向终点B运动,设运动时间为t(s).
如图,在矩形ABCD中,AB=4cm,AD=6cm,点P从点A出发,以1cm/s的速度沿AD向终点D运动,同时,点Q从点C出发,以1cm/s的速度沿CB向终点B运动,设运动时间为t(s).