题目内容
20.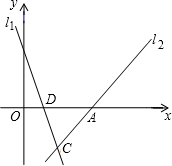 如图,已知直线l1:y=-3x+3与直线l2:y=mx-4m的图象的交点C在第四象限,且点C到y轴的距离为2.
如图,已知直线l1:y=-3x+3与直线l2:y=mx-4m的图象的交点C在第四象限,且点C到y轴的距离为2.(1)求直线l2的解析式;
(2)在第一象限的角平分线上是否存在点P,使得以P,A,O为顶点的三角形是直角三角形?如果存在,求出点P的坐标;如果不存在,请说明理由.
分析 (1)由直线直线l1解析式可滶得C点坐标,把C点坐标代入直线l2解析式可求得m的值,则可求得直线l2的解析式;
(2)作第一象限的角平分线OM,分∠PAO=90°和∠APO=90°,分别根据等腰直角三角形的性质可求得P点的坐标.
解答 解:
(1)在直线y=-3x+3中,当x=2时,y=-3,
∴点C的坐标为(2,-3),
把C点坐标代入直线l2的解析式可得2m-4m=-3,解得m=$\frac{3}{2}$,
∴直线l2的解析式为y=$\frac{3}{2}$x-6;
(2)存在.
如图1,作第一象限的角平分线OM,则∠MOA=45°,点P在OM上,
∴以点P、A、O为顶点的直角三角形分两种情况:
①当∠PAO=90°时,则有AO=PA,
∵直线l2与x轴交于点A,
∴A(4,0),
∴PA=OA=4,
∴P(4,4);
②当∠APO=90°时,则有AP=PO,过点P作PH⊥OA于点H,如图2,
∴OH=$\frac{1}{2}$AO=2,
∵∠POH=45°,∠OHP=90°,
∴∠OPH=∠POH=45°,
∴PH=OH=2,
∴P(2,2);
综上可知在第一象限的角平分线上存在点P使得△PAO是直角三角形,点P的坐标为(2,2)或(4,4).
点评 本题为一次函数的综合应用,涉及待定系数法、函数图象的交点、等腰直角三角形的性质、分类讨论思想等知识.在(1)中求得C点坐标是解题的关键,在(2)中确定出P点的位置是解题的关键,注意分两种情况.本题考查知识点较多,综合性较强,难度适中.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
11.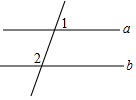 如图,已知直线a∥b,∠1=70°,那么∠2的度数是( )
如图,已知直线a∥b,∠1=70°,那么∠2的度数是( )
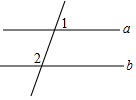 如图,已知直线a∥b,∠1=70°,那么∠2的度数是( )
如图,已知直线a∥b,∠1=70°,那么∠2的度数是( )| A. | 60° | B. | 80° | C. | 90° | D. | 110° |
5.函数y=$\frac{1}{x-2}$中,x的取值范围是( )
| A. | x≠2 | B. | x>2 | C. | x<2 | D. | x≠-2 |
12.2016年春节临近,武汉掀起购物狂潮,现有甲、乙、丙三个商场开展的促销活动如表所示:
根据以上活动信息,解决以下问题:
(1)三个商场同时出售一件标价290元的上一和一条标价270元的裤子,王阿姨想买这一套衣服,她应该选择哪家商场?完成表后就可以做出选择
(2)黄先生发现在甲、乙商场同时出售一件标价380元的上衣和一条标价300多元的裤子,最后付款额也一样,请问这条裤子的标价是多少元?
(3)丙商场又推出“先打折”,“再满100元减50元”的活动.张先生买了一件标价为630元的上衣,张先生发现竟然比没打折前多付了20元钱,问丙商场先打了多少折后再参加活动?(结果精确到0.01)
| 商场 | 优惠活动 |
| 甲 | 全场按标价的6折销售 |
| 乙 | 实行“满100元送100元的购物券”的优惠,购物券可以在再购买时冲抵现金 (比如:顾客购衣服220元,赠券200元,再购买裤子时可冲抵现金,不再送券) |
| 丙 | 实行“满100元减50元的优惠”(比如:某顾客购物220元,他只需付款120元) |
(1)三个商场同时出售一件标价290元的上一和一条标价270元的裤子,王阿姨想买这一套衣服,她应该选择哪家商场?完成表后就可以做出选择
| 商场 | 甲商场 | 乙商场 | 丙商场 |
| 实际付款(元) | 336 | 360 | 310 |
(3)丙商场又推出“先打折”,“再满100元减50元”的活动.张先生买了一件标价为630元的上衣,张先生发现竟然比没打折前多付了20元钱,问丙商场先打了多少折后再参加活动?(结果精确到0.01)
 如图是正方体的展开图,则原正方体相对两个面上的数字之和的最小值是6.
如图是正方体的展开图,则原正方体相对两个面上的数字之和的最小值是6.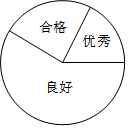 某校学生参加某项数学检测的成绩被分为优秀、良好、合格三个等级,其人数比为2:7:3,如图所示的扇形图表示上述分布情况.
某校学生参加某项数学检测的成绩被分为优秀、良好、合格三个等级,其人数比为2:7:3,如图所示的扇形图表示上述分布情况.