题目内容
5.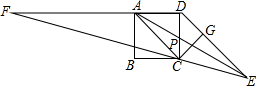 如图,四边形ABCD是正方形,DE∥AC,CE=AC,EC的延长线DA的延长线交于F,连AE交CD于P,作CG⊥DE于G,则下列结论:①AE平分∠CED;②S△ADP=S△EPC;③∠F=∠EAC;④CE=2CG.其中正确的说法有( )
如图,四边形ABCD是正方形,DE∥AC,CE=AC,EC的延长线DA的延长线交于F,连AE交CD于P,作CG⊥DE于G,则下列结论:①AE平分∠CED;②S△ADP=S△EPC;③∠F=∠EAC;④CE=2CG.其中正确的说法有( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 通过证明∠AED=∠AEC,即可得到AE平分∠CED;根据平行线之间的距离处处相等,即可得到S△ADC=S△AEC,进而得到S△ADP=S△EPC;通过计算得到∠F=15°,∠CAE=$\frac{1}{2}$ACF=15°,进而得出∠F=∠EAC;根据Rt△CEG中,∠CEG=30°,即可得出CE=2CG.
解答 解:∵DE∥AC,CE=AC,
∴∠AED=∠CAE,∠AEC=∠CAE,
∴∠AED=∠AEC,
即AE平分∠CED,故①正确;
∵AC∥DE,
∴S△ADC=S△AEC,
∴S△ADC-S△APC=S△AEC-S△APC
即S△ADP=S△EPC,故②正确;
∵∠CDG=∠ACD=45°,CG⊥DE,
∴△CDG是等腰直角三角形,
∵Rt△ACD中,AC=$\sqrt{2}$CD,Rt△CDG中,CD=$\sqrt{2}$G,
∴AC=2CG,即CE=2CG,
∴Rt△CEG中,∠CEG=30°,
∴∠ACF=∠CEG=30°,
又∵∠CAD=45°,
∴∠F=∠CAD-∠ACF=45°-30°=15°,
又∵∠CAE=$\frac{1}{2}$ACF=15°,
∴∠F=∠EAC,故③正确;
∵Rt△CEG中,∠CEG=30°,
∴CE=2CG,故④正确.
故选:D.
点评 本题主要考查了正方形的性质以及含30°角的直角三角形的性质,解题时注意:正方形两条对角线将正方形分成四个全等的等腰直角三角形,正方形是轴对称图形,有四条对称轴.

练习册系列答案
相关题目
17.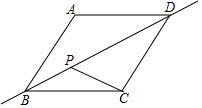 如图,菱形ABCD中,AB=2,∠A=120°,点P是直线BD上一动点,连接PC,当PC+$\frac{PB}{2}$的值最小时,线段PD的长是( )
如图,菱形ABCD中,AB=2,∠A=120°,点P是直线BD上一动点,连接PC,当PC+$\frac{PB}{2}$的值最小时,线段PD的长是( )
 如图,菱形ABCD中,AB=2,∠A=120°,点P是直线BD上一动点,连接PC,当PC+$\frac{PB}{2}$的值最小时,线段PD的长是( )
如图,菱形ABCD中,AB=2,∠A=120°,点P是直线BD上一动点,连接PC,当PC+$\frac{PB}{2}$的值最小时,线段PD的长是( )| A. | $\frac{4}{3}\sqrt{3}$ | B. | $\frac{2}{3}\sqrt{3}$ | C. | $2\sqrt{3}$ | D. | $\frac{4}{3}\sqrt{3}$ |
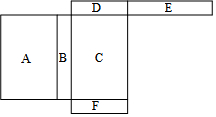 如图是一个长方体的表面展开图,每个面内都标出了字母,请根据要求回答问题.
如图是一个长方体的表面展开图,每个面内都标出了字母,请根据要求回答问题. 如图,在平面直角坐标系中,△ABC的两个顶点A,B的坐标分别为(-4,0),(-2,0),BC⊥x轴,将△ABC以y轴为对称轴作轴对称变换,得到△A'B'C'(A和A',B和B',C和C'分别是对应顶点),直线y=x+b经过点A、C',则点C'的坐标是(2,6).
如图,在平面直角坐标系中,△ABC的两个顶点A,B的坐标分别为(-4,0),(-2,0),BC⊥x轴,将△ABC以y轴为对称轴作轴对称变换,得到△A'B'C'(A和A',B和B',C和C'分别是对应顶点),直线y=x+b经过点A、C',则点C'的坐标是(2,6).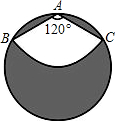 如图所示,有一个直径是1m的圆形铁皮,要从中剪出一个半径为$\frac{1}{2}$且圆心角是120°的扇形ABC.求被剪掉后剩余阴影部分的面积.
如图所示,有一个直径是1m的圆形铁皮,要从中剪出一个半径为$\frac{1}{2}$且圆心角是120°的扇形ABC.求被剪掉后剩余阴影部分的面积.