题目内容
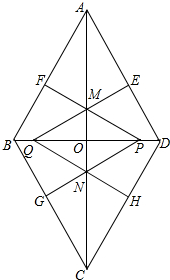 菱形ABCD的对角线AC,BD相交于点O,AC=4
菱形ABCD的对角线AC,BD相交于点O,AC=4| 3 |
(1)用含x的代数式分别表示S1,S2;
(2)若S1=S2,求x的值.
考点:四边形综合题,菱形的性质,轴对称的性质,轴对称图形,特殊角的三角函数值
专题:综合题,压轴题,动点型,分类讨论
分析:(1)根据对称性确定E、F、G、H都在菱形的边上,由于点P在BO上与点P在OD上求S1和S2的方法不同,因此需分情况讨论.
(2)由S1=S2和S1+S2=8
可以求出S1=S2=4
.然后在两种情况下分别建立关于x的方程,解方程,结合不同情况下x的范围确定x的值.
(2)由S1=S2和S1+S2=8
| 3 |
| 3 |
解答: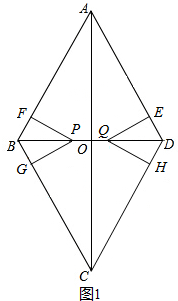 解:(1)①当点P在BO上,0<x≤2时,如图1所示.
解:(1)①当点P在BO上,0<x≤2时,如图1所示.
∵四边形ABCD是菱形,AC=4
,BD=4,
∴AC⊥BD,BO=
BD=2,AO=
AC=2
,
且S菱形ABCD=
BD•AC=8
.
∴tan∠ABO=
=
.
∴∠ABO=60°.
在Rt△BFP中,
∵∠BFP=90°,∠FBP=60°,BP=x,
∴sin∠FBP=
=
=sin60°=
.
∴FP=
x.
∴BF=
.
∵四边形PFBG关于BD对称,
四边形QEDH与四边形PEBG关于AC对称,
∴S△BFP=S△BGP=S△DEQ=S△DHQ.
∴S1=4S△BFP
=4×
×
x•
=
x2.
∴S2=8
-
x2.
②当点P在OD上,2<x≤4时,如图2所示.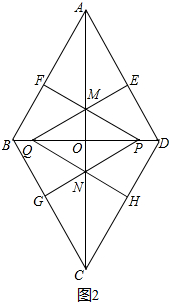
∵AB=4,BF=
,
∴AF=AB-BF=4-
.
在Rt△AFM中,
∵∠AFM=90°,∠FAM=30°,AF=4-
.
∴tan∠FAM=
=tan30°=
.
∴FM=
(4-
).
∴S△AFM=
AF•FM
=
(4-
)•
(4-
)
=
(4-
)2.
∵四边形PFBG关于BD对称,
四边形QEDH与四边形PEBG关于AC对称,
∴S△AFM=S△AEM=S△CHN=S△CGN.
∴S2=4S△AFM
=4×
(4-
)2
=
(x-8)2.
∴S1=8
-S2=8
-
(x-8)2.
综上所述:
当0<x≤2时,S1=
x2,S2=8
-
x2;
当2<x≤4时,S1=8
-
(x-8)2,S2=
(x-8)2.
(2)①当点P在BO上时,0<x≤2.
∵S1=S2,S1+S2=8
,
∴S1=4
.
∴S1=
x2=4
.
解得:x1=2
,x2=-2
.
∵2
>2,-2
<0,
∴当点P在BO上时,S1=S2的情况不存在.
②当点P在OD上时,2<x≤4.
∵S1=S2,S1+S2=8
,
∴S2=4
.
∴S2=
(x-8)2=4
.
解得:x1=8+2
,x2=8-2
.
∵8+2
>4,2<8-2
<4,
∴x=8-2
.
综上所述:若S1=S2,则x的值为8-2
.
 解:(1)①当点P在BO上,0<x≤2时,如图1所示.
解:(1)①当点P在BO上,0<x≤2时,如图1所示.∵四边形ABCD是菱形,AC=4
| 3 |
∴AC⊥BD,BO=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
且S菱形ABCD=
| 1 |
| 2 |
| 3 |
∴tan∠ABO=
| AO |
| BO |
| 3 |
∴∠ABO=60°.
在Rt△BFP中,
∵∠BFP=90°,∠FBP=60°,BP=x,
∴sin∠FBP=
| FP |
| BP |
| FP |
| x |
| ||
| 2 |
∴FP=
| ||
| 2 |
∴BF=
| x |
| 2 |
∵四边形PFBG关于BD对称,
四边形QEDH与四边形PEBG关于AC对称,
∴S△BFP=S△BGP=S△DEQ=S△DHQ.
∴S1=4S△BFP
=4×
| 1 |
| 2 |
| ||
| 2 |
| x |
| 2 |
=
| ||
| 2 |
∴S2=8
| 3 |
| ||
| 2 |
②当点P在OD上,2<x≤4时,如图2所示.

∵AB=4,BF=
| x |
| 2 |
∴AF=AB-BF=4-
| x |
| 2 |
在Rt△AFM中,
∵∠AFM=90°,∠FAM=30°,AF=4-
| x |
| 2 |
∴tan∠FAM=
| FM |
| AF |
| ||
| 3 |
∴FM=
| ||
| 3 |
| x |
| 2 |
∴S△AFM=
| 1 |
| 2 |
=
| 1 |
| 2 |
| x |
| 2 |
| ||
| 3 |
| x |
| 2 |
=
| ||
| 6 |
| x |
| 2 |
∵四边形PFBG关于BD对称,
四边形QEDH与四边形PEBG关于AC对称,
∴S△AFM=S△AEM=S△CHN=S△CGN.
∴S2=4S△AFM
=4×
| ||
| 6 |
| x |
| 2 |
=
| ||
| 6 |
∴S1=8
| 3 |
| 3 |
| ||
| 6 |
综上所述:
当0<x≤2时,S1=
| ||
| 2 |
| 3 |
| ||
| 2 |
当2<x≤4时,S1=8
| 3 |
| ||
| 6 |
| ||
| 6 |
(2)①当点P在BO上时,0<x≤2.
∵S1=S2,S1+S2=8
| 3 |
∴S1=4
| 3 |
∴S1=
| ||
| 2 |
| 3 |
解得:x1=2
| 2 |
| 2 |
∵2
| 2 |
| 2 |
∴当点P在BO上时,S1=S2的情况不存在.
②当点P在OD上时,2<x≤4.
∵S1=S2,S1+S2=8
| 3 |
∴S2=4
| 3 |
∴S2=
| ||
| 6 |
| 3 |
解得:x1=8+2
| 6 |
| 6 |
∵8+2
| 6 |
| 6 |
∴x=8-2
| 6 |
综上所述:若S1=S2,则x的值为8-2
| 6 |
点评:本题考查了以菱形为背景的轴对称及轴对称图形的相关知识,考查了菱形的性质、特殊角的三角函数值等知识,还考查了分类讨论的思想.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
分式
可变形为( )
| 2 |
| 2-x |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
 随着人民生活水平的提高,购买老年代步车的人越来越多.这些老年代步车却成为交通安全的一大隐患.针对这种现象,某校数学兴趣小组在《老年代步车现象的调查报告》中就“你认为对老年代步车最有效的管理措施”随机对某社区部分居民进行了问卷调查,其中调查问卷设置以下选项(只选一项):
随着人民生活水平的提高,购买老年代步车的人越来越多.这些老年代步车却成为交通安全的一大隐患.针对这种现象,某校数学兴趣小组在《老年代步车现象的调查报告》中就“你认为对老年代步车最有效的管理措施”随机对某社区部分居民进行了问卷调查,其中调查问卷设置以下选项(只选一项):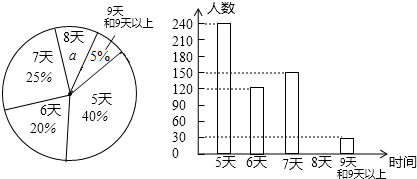
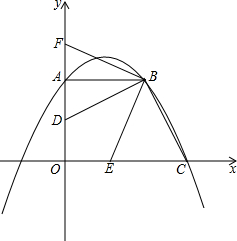 如图,在平面直角坐标系中,点A在y轴的正半轴上,点B在第一象限,点C的坐标为(3,0).AB∥x轴,且OA=AB,抛物线y=ax2+bx+2经过点A、B、C.连 结BC,过点B作BD⊥BC,交OA于点D.将∠CBD绕点B按顺时针方向旋转得到∠EBF,角的两边分别交x轴的正半轴、y轴的正半轴于E、F.
如图,在平面直角坐标系中,点A在y轴的正半轴上,点B在第一象限,点C的坐标为(3,0).AB∥x轴,且OA=AB,抛物线y=ax2+bx+2经过点A、B、C.连 结BC,过点B作BD⊥BC,交OA于点D.将∠CBD绕点B按顺时针方向旋转得到∠EBF,角的两边分别交x轴的正半轴、y轴的正半轴于E、F. 某校男生、女生以及教师人数的扇形统计图如图所示,若该校师生的总人数为1500人,结合图中信息,可得该校教师人数为
某校男生、女生以及教师人数的扇形统计图如图所示,若该校师生的总人数为1500人,结合图中信息,可得该校教师人数为