题目内容
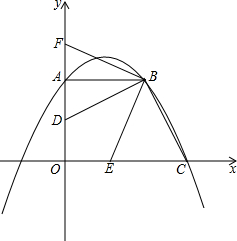 如图,在平面直角坐标系中,点A在y轴的正半轴上,点B在第一象限,点C的坐标为(3,0).AB∥x轴,且OA=AB,抛物线y=ax2+bx+2经过点A、B、C.连 结BC,过点B作BD⊥BC,交OA于点D.将∠CBD绕点B按顺时针方向旋转得到∠EBF,角的两边分别交x轴的正半轴、y轴的正半轴于E、F.
如图,在平面直角坐标系中,点A在y轴的正半轴上,点B在第一象限,点C的坐标为(3,0).AB∥x轴,且OA=AB,抛物线y=ax2+bx+2经过点A、B、C.连 结BC,过点B作BD⊥BC,交OA于点D.将∠CBD绕点B按顺时针方向旋转得到∠EBF,角的两边分别交x轴的正半轴、y轴的正半轴于E、F.(1)求a、b的值.
(2)当直线BF经过抛物线y=ax2+bx+2的顶点时,求CE的长.
(3)连结EF.设△BEF与△BEC的面积之差为S.当CE为何值时S最小,求出这个最小值.
考点:二次函数综合题
专题:
分析:(1)把点B、C的坐标分别代入抛物线解析式,列出关于a、b的方程组,通过解方程组来求它们的值;
(2)如图,过点G作GH⊥AB于点H,过点B作BM⊥OC于点M.构建全等三角形:△EBM≌△FBA(AAS).则EM=AF.tan∠ABF=
=
,易求AF=
.故CE=CM+EM=1+
=
;
(3)设CE=m,则EM=m-1或1-m.在直角△BEM中,利用勾股定理得到BE2=EM2+BM2=m2-2m+5.又由(2)中的全等三角形的对应边相等推知:BF=BE.易求S=
(m-2)2+
.根据抛物线的性质知:当m=2时,S最小=
.
(2)如图,过点G作GH⊥AB于点H,过点B作BM⊥OC于点M.构建全等三角形:△EBM≌△FBA(AAS).则EM=AF.tan∠ABF=
| AF |
| AB |
| HG |
| HB |
| 4 |
| 3 |
| 4 |
| 3 |
| 7 |
| 3 |
(3)设CE=m,则EM=m-1或1-m.在直角△BEM中,利用勾股定理得到BE2=EM2+BM2=m2-2m+5.又由(2)中的全等三角形的对应边相等推知:BF=BE.易求S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答: 解:(1)根据题意,B(2,2),C(3,0),则
解:(1)根据题意,B(2,2),C(3,0),则
,
解得
;
(2)由(1)知,经过A、B、C的抛物线为y=-
x2+
x+2.
故顶点G的坐标为(1,
).
如图,过点G作GH⊥AB于点H,
则AH=BH=1,GH=
-2=
.
过点B作BM⊥OC于点M.则四边形ABMO为正方形.
∴BA=BM.
∵∠ABM=∠EBF=90°,
∴∠EBM=∠FBA.
∵∠BME=∠BAF=90°,
∴在△EBM与△FBA中,
,
∴△EBM≌△FBA(AAS).
∴EM=AF.
∵tan∠ABF=
=
,
∴AF=
.
∴EM=AF=
.
又∵C(3,0),B(2,2),
∴CM=1.
∴CE=CM+EM=1+
=
;
(3)如图,连接EF.
设CE=m,则EM=m-1或1-m,
∴BE2=EM2+BM2=(m-1)2+2 2=m2-2m+5.
又∵△FBA≌△EBM,
∴BF=BE.
∴S=S△BEF-S△BEC.
即S=
(m-2)2+
.
当m=2时,S最小=
.
 解:(1)根据题意,B(2,2),C(3,0),则
解:(1)根据题意,B(2,2),C(3,0),则
|
解得
|
(2)由(1)知,经过A、B、C的抛物线为y=-
| 2 |
| 3 |
| 4 |
| 3 |
故顶点G的坐标为(1,
| 8 |
| 3 |
如图,过点G作GH⊥AB于点H,
则AH=BH=1,GH=
| 8 |
| 3 |
| 2 |
| 3 |
过点B作BM⊥OC于点M.则四边形ABMO为正方形.
∴BA=BM.
∵∠ABM=∠EBF=90°,
∴∠EBM=∠FBA.
∵∠BME=∠BAF=90°,
∴在△EBM与△FBA中,
|
∴△EBM≌△FBA(AAS).
∴EM=AF.
∵tan∠ABF=
| AF |
| AB |
| HG |
| HB |
∴AF=
| 4 |
| 3 |
∴EM=AF=
| 4 |
| 3 |
又∵C(3,0),B(2,2),
∴CM=1.
∴CE=CM+EM=1+
| 4 |
| 3 |
| 7 |
| 3 |
(3)如图,连接EF.
设CE=m,则EM=m-1或1-m,
∴BE2=EM2+BM2=(m-1)2+2 2=m2-2m+5.
又∵△FBA≌△EBM,
∴BF=BE.
∴S=S△BEF-S△BEC.
即S=
| 1 |
| 2 |
| 1 |
| 2 |
当m=2时,S最小=
| 1 |
| 2 |
点评:本题是二次函数的综合题型,其中涉及到的知识点有待定系数法求二次函数解析式,坐标与图形的性质,勾股定理,全等三角形的判定与性质以及三角形的面积求法等.该题综合性比较强,难度较大.解题时,要注意数形结合的数学思想方法的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
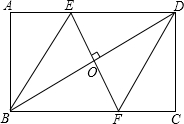 如图,在矩形ABCD中,边AB的长为3,点E,F分别在AD,BC上,连接BE,DF,EF,BD.若四边形BEDF是菱形,且EF=AE+FC,则边BC的长为( )
如图,在矩形ABCD中,边AB的长为3,点E,F分别在AD,BC上,连接BE,DF,EF,BD.若四边形BEDF是菱形,且EF=AE+FC,则边BC的长为( ) 为提高居民的节水意识,向阳小区开展了“建设节水型社区,保障用水安全”为主题的节水宣传活动,小莹同学积极参与小区的宣传活动,并对小区300户家庭用水情况进行了抽样调查,他在300户家庭中,随机调查了50户家庭5月份的用水量情况,结果如图所示.
为提高居民的节水意识,向阳小区开展了“建设节水型社区,保障用水安全”为主题的节水宣传活动,小莹同学积极参与小区的宣传活动,并对小区300户家庭用水情况进行了抽样调查,他在300户家庭中,随机调查了50户家庭5月份的用水量情况,结果如图所示.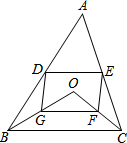 D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点.O是△ABC所在平面上的动点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点.O是△ABC所在平面上的动点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E. 如图,已知矩形ABCD的边AB=1,M是边AD上的动点,直线l过M与对角线AC垂直,垂足为E,且
如图,已知矩形ABCD的边AB=1,M是边AD上的动点,直线l过M与对角线AC垂直,垂足为E,且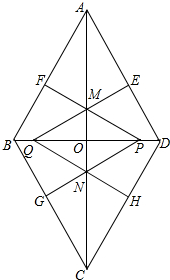 菱形ABCD的对角线AC,BD相交于点O,AC=4
菱形ABCD的对角线AC,BD相交于点O,AC=4