题目内容
已知:如图,在△ABC中,点A1,B1,C1分别是BC、AC、AB的中点,A2,B2,C2分别是B1C1,A1C1,A1B1的中点,依此类推….若△ABC的周长为1,则△AnBnCn的周长为 .
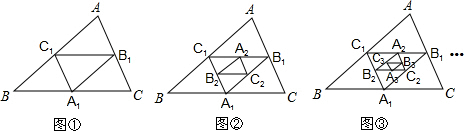

考点:三角形中位线定理
专题:规律型
分析:由于A1、B1、C1分别是△ABC的边BC、CA、AB的中点,就可以得出△A1B1C1∽△ABC,且相似比为
,△A2B2C2∽△ABC的相似比为
,依此类推△AnBnCn∽△ABC的相似比为
,
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2n |
解答:解:∵A1、B1、C1分别是△ABC的边BC、CA、AB的中点,
∴A1B1、A1C1、B1C1是△ABC的中位线,
∴△A1B1C1∽△ABC,且相似比为
,
∵A2、B2、C2分别是△A1B1C1的边B1C1、C1A1、A1B1的中点,
∴△A2B2C2∽△A1B1C1且相似比为
,
∴△A2B2C2∽△ABC的相似比为
依此类推△AnBnCn∽△ABC的相似比为
,
∵△ABC的周长为1,
∴△AnBnCn的周长为
.
故答案为:
.
∴A1B1、A1C1、B1C1是△ABC的中位线,
∴△A1B1C1∽△ABC,且相似比为
| 1 |
| 2 |
∵A2、B2、C2分别是△A1B1C1的边B1C1、C1A1、A1B1的中点,
∴△A2B2C2∽△A1B1C1且相似比为
| 1 |
| 2 |
∴△A2B2C2∽△ABC的相似比为
| 1 |
| 4 |
依此类推△AnBnCn∽△ABC的相似比为
| 1 |
| 2n |
∵△ABC的周长为1,
∴△AnBnCn的周长为
| 1 |
| 2n |
故答案为:
| 1 |
| 2n |
点评:本题考查了三角形中位线定理的运用,相似三角形的判定与性质的运用,解题的关键是熟练运用相似三角形的性质.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
 为提高居民的节水意识,向阳小区开展了“建设节水型社区,保障用水安全”为主题的节水宣传活动,小莹同学积极参与小区的宣传活动,并对小区300户家庭用水情况进行了抽样调查,他在300户家庭中,随机调查了50户家庭5月份的用水量情况,结果如图所示.
为提高居民的节水意识,向阳小区开展了“建设节水型社区,保障用水安全”为主题的节水宣传活动,小莹同学积极参与小区的宣传活动,并对小区300户家庭用水情况进行了抽样调查,他在300户家庭中,随机调查了50户家庭5月份的用水量情况,结果如图所示.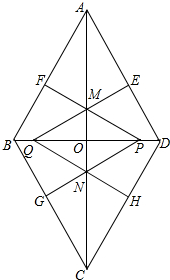 菱形ABCD的对角线AC,BD相交于点O,AC=4
菱形ABCD的对角线AC,BD相交于点O,AC=4
 如图1,折线段AOB将面积为S的⊙O分成两个扇形,大扇形、小扇形的面积分别为S1、S2,若
如图1,折线段AOB将面积为S的⊙O分成两个扇形,大扇形、小扇形的面积分别为S1、S2,若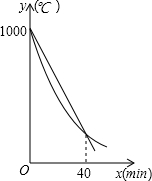 某研究所将某种材料加热到1000℃时停止加热,并立即将材料分为A、B两组,采用不同工艺做降温对比实验,设降温开始后经过x min时,A、B两组材料的温度分别为yA℃、yB℃,yA、yB与x的函数关系式分别为yA=kx+b,yB=
某研究所将某种材料加热到1000℃时停止加热,并立即将材料分为A、B两组,采用不同工艺做降温对比实验,设降温开始后经过x min时,A、B两组材料的温度分别为yA℃、yB℃,yA、yB与x的函数关系式分别为yA=kx+b,yB=