题目内容
19．
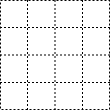在4×4的方格中，△ABC的三个顶点均在格点上，其中AB=$\sqrt{5}$，BC=2$\sqrt{2}$，AC=$\sqrt{17}$．则△ABC中AC边上的高的长为$\frac{6\sqrt{17}}{17}$．（保留根号）
分析 首先作出△ABC，用梯形面积-两个小三角形面积求得△ABC的面积，再根据三角形面积公式即可求解．
解答 解：如图：
△ABC的面积=$\frac{1}{2}$×（2+4）×2-$\frac{1}{2}$×2×1-$\frac{1}{2}$×4×1
=6-1-2
=3，
△ABC中AC边上的高的长为3×2÷$\sqrt{17}$=$\frac{6\sqrt{17}}{17}$．
故答案为：$\frac{6\sqrt{17}}{17}$．
点评 此题考查了勾股定理，以及三角形的面积，熟练掌握勾股定理作出△ABC是解本题的关键．
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
7．实数$\root{3}{27}$，0，$\frac{1}{7}$，-π，$\sqrt{16}$，$\sqrt{6}$，0.1010010001…（相邻两个1之间依次多一个0），其中，无理数有（ ）个．
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
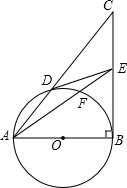如图，在△ABC中，∠B=90°，以AB为直径的⊙O交AC于点D，过点D作⊙O的切线交BC于E，连接AE交⊙O于点F．