题目内容
11．如果不等式组$\left\{\begin{array}{l}{2x-5＞3（x-1）}\\{-x＜m}\end{array}\right.$的解集是无解，那么m的取值范围是（ ）| A． | m=2 | B． | m≥2 | C． | m＜2 | D． | m≤2 |
分析 首先解每个不等式，然后根据不等式组无解即可得到一个关于m的不等式，求得m的范围．
解答 解：$\left\{\begin{array}{l}{2x-5＞3（x-1）…①}\\{-x＜m…②}\end{array}\right.$，
解①得：x＜-2，
解②得：x＞-m．
根据题意得：-m≥-2，
解得：m≤2．
故选B．
点评 本题考查的是一元一次不等式组的解，解此类题目常常要结合数轴来判断．还可以观察不等式的解，若x＞较小的数、＜较大的数，那么解集为x介于两数之间．
练习册系列答案
学业测评一课一测系列答案
相关题目
1．
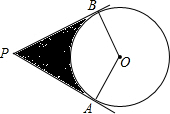如图，过半径为2$\sqrt{3}$的⊙O外一点P引⊙O的切线PA、PB，切点为A、B，如果∠APB=60°，则图中阴影的面积等于（ ）
如图，过半径为2$\sqrt{3}$的⊙O外一点P引⊙O的切线PA、PB，切点为A、B，如果∠APB=60°，则图中阴影的面积等于（ ）| A． | 12$\sqrt{3}$-4π | B． | 24$\sqrt{3}$-4π | C． | 12$\sqrt{3}$-2π | D． | 24$\sqrt{3}$-2π |
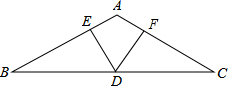如图，在△ABC中，AB=AC，D是BC边上的点，DE⊥AB，DF⊥AC，垂足分别为E，F，∠BAC=120°，BC=12，求DE+DF的值．
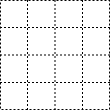在4×4的方格中，△ABC的三个顶点均在格点上，其中AB=$\sqrt{5}$，BC=2$\sqrt{2}$，AC=$\sqrt{17}$．则△ABC中AC边上的高的长为$\frac{6\sqrt{17}}{17}$．（保留根号）
如图，在函数y=$\frac{8}{x}$（x＞0）的图象上有点P1、P2、P3…、Pn、Pn+1，点P1的横坐标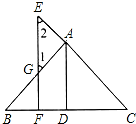
已知：如图，AD⊥BC于D，EF⊥BC于F，交AB于G，交CA延长线于E，∠1=∠2．
在Rt△ABC中，∠C=90°，D、E分别为AB、BC上的点，且BD•AB=BE•BC．