题目内容
8.计算或化简:(1)($\sqrt{48}$-$\sqrt{75}$)×$\sqrt{1\frac{1}{3}}$;
(2)($\frac{x+1}{{x}^{2}-x}$-$\frac{x}{{x}^{2}-2x+1}$)÷$\frac{1}{x}$.
分析 (1)先把各二次根式化为最简二次根式,然后把括号内合并后进行二次根式的乘法运算;
(2)先把分子分母分解因式和除法运算化为乘法运算,再把括号内通分后进行减法运算,然后约分即可.
解答 解:(1)原式=(4$\sqrt{3}$-5$\sqrt{3}$)×$\frac{2\sqrt{3}}{3}$
=-$\sqrt{3}$×$\frac{2\sqrt{3}}{3}$
=-2;
(2)原式=[$\frac{x+1}{x(x-1)}$-$\frac{x}{(x-1)^{2}}$]•x
=$\frac{(x+1)(x-1)-{x}^{2}}{x(x-1)^{2}}$•x
=$\frac{{x}^{2}-1-{x}^{2}}{x(x-1)^{2}}$•x
=-$\frac{1}{{x}^{2}-2x+1}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了分式的混合运算.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
18.在下列条件中,能画出平行四边形的是( )
| A. | 以60cm为一条对角线,20cm和34cm为两条邻边 | |
| B. | 以6cm和10cm为对角线,8cm为一条边 | |
| C. | 以20cm和36cm为对角线,22cm为一条边 | |
| D. | 以6cm为一条对角线,3cm和10cm为两条邻边 |
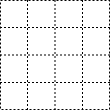 在4×4的方格中,△ABC的三个顶点均在格点上,其中AB=$\sqrt{5}$,BC=2$\sqrt{2}$,AC=$\sqrt{17}$.则△ABC中AC边上的高的长为$\frac{6\sqrt{17}}{17}$.(保留根号)
在4×4的方格中,△ABC的三个顶点均在格点上,其中AB=$\sqrt{5}$,BC=2$\sqrt{2}$,AC=$\sqrt{17}$.则△ABC中AC边上的高的长为$\frac{6\sqrt{17}}{17}$.(保留根号)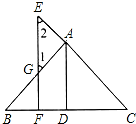 已知:如图,AD⊥BC于D,EF⊥BC于F,交AB于G,交CA延长线于E,∠1=∠2.
已知:如图,AD⊥BC于D,EF⊥BC于F,交AB于G,交CA延长线于E,∠1=∠2.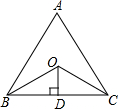 如图,BO、CO分别平分∠ABC、∠ACB,OD⊥BC于点D.
如图,BO、CO分别平分∠ABC、∠ACB,OD⊥BC于点D.