题目内容
已知△ABC中,AB=5,AC=12,BC=13.
(1)△ABC是什么三角形?并证明.
(2)求出BC边上的高.
(1)△ABC是什么三角形?并证明.
(2)求出BC边上的高.
考点:勾股定理的逆定理
专题:
分析:(1)根据勾股定理的逆定理即可判定△ABC是直角三角形;
(2)利用面积法即可求出BC边上的高.
(2)利用面积法即可求出BC边上的高.
解答:解:(1)△ABC是直角三角形,理由如下:
∵AB=5,AC=12,BC=13,
∴AB2+AC2=25+144=169=BC2,
∴△ABC为直角三角形;
(2)设BC边上的高为h,
∵△ABC的面积=
BC•h=
AB•AC,
∴h=
=
=
.
∵AB=5,AC=12,BC=13,
∴AB2+AC2=25+144=169=BC2,
∴△ABC为直角三角形;
(2)设BC边上的高为h,
∵△ABC的面积=
| 1 |
| 2 |
| 1 |
| 2 |
∴h=
| AB•AC |
| BC |
| 5×12 |
| 13 |
| 60 |
| 13 |
点评:本题考查勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.同时考查了三角形的面积.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案
相关题目
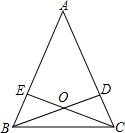 如图,已知AB=AC,AE=AD,则①△ABD≌△ACE,②△BOE≌△COD,③点O在∠BAC的平分线上,( )
如图,已知AB=AC,AE=AD,则①△ABD≌△ACE,②△BOE≌△COD,③点O在∠BAC的平分线上,( )| A、都正确 |
| B、都不正确 |
| C、只有一个正确 |
| D、只有一个不正确 |
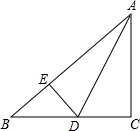 如图所示,已知AC⊥BC,AD平分∠BAC,DE⊥AB,那么下列等式不成立的是( )
如图所示,已知AC⊥BC,AD平分∠BAC,DE⊥AB,那么下列等式不成立的是( )| A、∠ADE=∠ADC |
| B、∠BAC=∠BDE |
| C、DC=DE |
| D、∠ADE=∠BDE |
函数y=(2m-1)xn+3+(m-5)是关于x的一次函数的条件为( )
| A、m≠5且n=-2 | ||
| B、n=-2 | ||
C、m≠
| ||
D、m≠
|
 如图,以数轴的单位长度线段为边作一个正方形,以表示数1的点为圆心,正方形对角线长为半径画弧,交数轴于点A,则点A表示的数是
如图,以数轴的单位长度线段为边作一个正方形,以表示数1的点为圆心,正方形对角线长为半径画弧,交数轴于点A,则点A表示的数是 如图,△ABC中,∠C=36°,∠B=72°,EF∥AB.四边形ABEF是等腰梯形吗?为什么?
如图,△ABC中,∠C=36°,∠B=72°,EF∥AB.四边形ABEF是等腰梯形吗?为什么?