题目内容
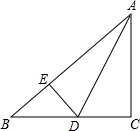 如图所示,已知AC⊥BC,AD平分∠BAC,DE⊥AB,那么下列等式不成立的是( )
如图所示,已知AC⊥BC,AD平分∠BAC,DE⊥AB,那么下列等式不成立的是( )| A、∠ADE=∠ADC |
| B、∠BAC=∠BDE |
| C、DC=DE |
| D、∠ADE=∠BDE |
考点:角平分线的性质,全等三角形的判定与性质
专题:
分析:根据角平分线性质和垂线定义得出∠EAD=∠CAD,DE=DC,∠C=∠AED=∠BED=90°,根据三角形内角和定理即可判断A、B;根据DC=DE即可判断C;根据图形和已知即可判断D.
解答:解:∵AC⊥BC,AD平分∠BAC,DE⊥AB,
∴∠EAD=∠CAD,DE=DC,∠C=∠AED=∠BED=90°,
A、∵∠C=∠AED=∠BED=90°,∠EAD=∠CAD,∠AED+∠EAD+∠ADE=180°,∠CAD+∠ADC+C=180°,
∴∠ADE=∠ADC,故版本选项错误;
B、∵∠C=∠BED=90°,
∴∠B+∠BAC=90°,∠B+∠BDE=90°,
∴∠BAC=∠BDE,故本选项错误;
C、∵DC=DE,故本选项错误;
D、根据已知不能推出∠ADE∠BDE,故本选项正确;
故选D.
∴∠EAD=∠CAD,DE=DC,∠C=∠AED=∠BED=90°,
A、∵∠C=∠AED=∠BED=90°,∠EAD=∠CAD,∠AED+∠EAD+∠ADE=180°,∠CAD+∠ADC+C=180°,
∴∠ADE=∠ADC,故版本选项错误;
B、∵∠C=∠BED=90°,
∴∠B+∠BAC=90°,∠B+∠BDE=90°,
∴∠BAC=∠BDE,故本选项错误;
C、∵DC=DE,故本选项错误;
D、根据已知不能推出∠ADE∠BDE,故本选项正确;
故选D.
点评:本题考查了三角形内角和定理和角平分线性质的应用,主要考查学生运用定理进行推理的能力,注意:角平分线上的点到角两边的距离相等.

练习册系列答案
相关题目
 如图,在4×4方格中画以AB为一边的Rt△ABC,要求点C也在格点上,这样的点C一共可以画出( )
如图,在4×4方格中画以AB为一边的Rt△ABC,要求点C也在格点上,这样的点C一共可以画出( )| A、4个 | B、5个 | C、6个 | D、8个 |
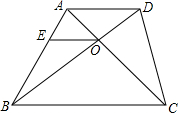 如图,在梯形ABCD中,AD∥BC,对角线AC与BD相交于点O,过点O作OE∥AD交AB于点E.若AD=6cm,BC=12cm,△AOD的面积为6cm2,
如图,在梯形ABCD中,AD∥BC,对角线AC与BD相交于点O,过点O作OE∥AD交AB于点E.若AD=6cm,BC=12cm,△AOD的面积为6cm2,
 以直线为对称轴,画出下列图形的另一部分使它们成为轴对称图形.
以直线为对称轴,画出下列图形的另一部分使它们成为轴对称图形.