题目内容
2.已知关于x的方程$\sqrt{x}=x+k$有两个不同的实数根,则实数k的取值范围是0≤k<$\frac{1}{4}$.分析 根据平方,可得一元二次方程,根据根的判别式,根与系数的关系,可得不等式组,根据解不等式组,可得答案.
解答 解:平方,得
x=(x+k)2,
化简,得
x2+(2k-1)x+k2=0,
由关于x的方程$\sqrt{x}=x+k$有两个不同的非负实数根,得
$\left\{\begin{array}{l}{(2k-1)^{2}-4{k}^{2}>0}\\{1-2k≥0}\end{array}\right.$,
解得0≤k<$\frac{1}{4}$.
故答案为:0≤k<$\frac{1}{4}$.
点评 本题考查了无理方程,利用平方得出整式方程是解题关键,又利用判别式,根与系数的关系得出不等式组.

练习册系列答案
相关题目
12.下列说法正确的是( )
| A. | $\sqrt{4}$的平方根是±2 | B. | -$\sqrt{2}$表示2的算术平方根的相反数 | ||
| C. | -a2一定没有算术平方根 | D. | 0.9的算术平方根是0.3 |
 “赵爽弦图”是四个全等的直角三角形与中间一个正方形拼成的大正方形.如图,每一个直角三角形的两条直角边的长分别是3和6,则中间小正方形与大正方形的面积差是( )
“赵爽弦图”是四个全等的直角三角形与中间一个正方形拼成的大正方形.如图,每一个直角三角形的两条直角边的长分别是3和6,则中间小正方形与大正方形的面积差是( )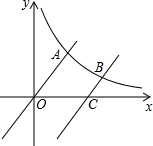 如图,已知函数y=x与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点A,将y=x的图象向下平移6个单位后与双曲线y=$\frac{m}{x}$交于点B,与x轴交于点C,若$\frac{OA}{CB}$=2,则m的值为( )
如图,已知函数y=x与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点A,将y=x的图象向下平移6个单位后与双曲线y=$\frac{m}{x}$交于点B,与x轴交于点C,若$\frac{OA}{CB}$=2,则m的值为( )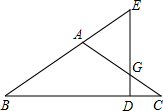 如图,在△ABC中,AB=AC,过AC上的一点G作GD⊥BC于点D,交BA的延长线于点E.
如图,在△ABC中,AB=AC,过AC上的一点G作GD⊥BC于点D,交BA的延长线于点E.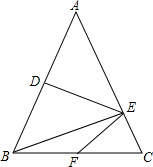 如图,已知在△ABC中,AB=AC,DE垂直平分AB,垂足为点D,连接BE,BE⊥AC.
如图,已知在△ABC中,AB=AC,DE垂直平分AB,垂足为点D,连接BE,BE⊥AC.