题目内容
10.过矩形ABCD的顶点C作CE⊥BD于E,若矩形的两条对角线所夹的锐角为45°,则∠BCE与∠DCE的比是3:1.分析 设两对角线交点为O,由矩形的性质和已知条件分别求出∠BCE与∠DCE的度数即可得到其角大小的比值.
解答 解:
设两对角线交点为O,
∵四边形ABCD是矩形,
∴OB=OC,∠BCD=90°,
∵∠DOC=45°,CE⊥BD于E,
∴∠ECO=45°,∠BOC=135°,
∴∠BCO=∠CBO=22.5°,
∴∠BCE=67.5°,
∴∠DCE=22.5°
∴∠BCE和∠ECD的度数之比为3:1,
故答案为3:1.
点评 本题考查了矩形的性质以及三角形内角和定理的运用,熟记矩形的各种性质是解题的关键.

练习册系列答案
相关题目
18.数据3,5,4,5,6的中位数和众数分别是( )
| A. | 4,5 | B. | 5,5 | C. | 5,4 | D. | 4,6 |
5.已知m<0,关于x的方程(x-2)2-m=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 有两个实数根 |
15.在$\frac{23}{7}$,3.141,$\sqrt{6}$,-3,$\root{3}{5}$,0,3.2,$\sqrt{25}$,$\frac{π}{6}$中是无理数的个数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
2.方程2x-y=3和2x+y=9的公共解是( )
| A. | $\left\{\begin{array}{l}{x=0}\\{y=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=3}\\{y=-3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=1}\\{y=7}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=3}\\{y=3}\end{array}\right.$ |
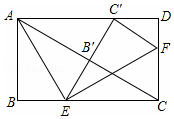 如图,在矩形ABCD中,点E,F分别在BC,CD上,将△ABE沿AE折叠,使点B落在AC上的点B′处,又将△CEF沿EF折叠,使点C落在EB′与AD的交点C′处.则CF:AB的值为2:3.
如图,在矩形ABCD中,点E,F分别在BC,CD上,将△ABE沿AE折叠,使点B落在AC上的点B′处,又将△CEF沿EF折叠,使点C落在EB′与AD的交点C′处.则CF:AB的值为2:3.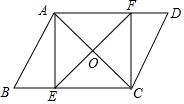 如图,在?ABCD中,AB=4cm,AD=6cm,点E、F是?ABCD边BC、AD上的两点,BE=DF,AC,EF相交于点O,若AC⊥EF,则△ABE的周长为10cm.
如图,在?ABCD中,AB=4cm,AD=6cm,点E、F是?ABCD边BC、AD上的两点,BE=DF,AC,EF相交于点O,若AC⊥EF,则△ABE的周长为10cm.