题目内容
4.若x4-5x3+ax2+bx+c能被(x-1)2整除,试求(a+b+c)2的值.分析 由于多项式x4-5x3+ax2+bx+c能被多项式(x-1)2整除,则说明(x-1)2=0,求出的x也能使x4-5x3+ax2+bx+c=0,从而得到关于a、b、c的两个等式,对两个等式变形,可得4a+c=12③;
解答 解:∵x4-5x3+ax2+bx+c能被(x-1)2整除,
∴(x-1)2=0,
解得:x=1,
即x=1是方程x4-5x3+ax2+bx+c=0的解,
∴1-5+a+b+c=0,
∴a+b+c=4,
∴(a+b+c)2=42=16.
点评 本题考查的是多项式除以多项式,注意理解整除的含义,比如A被B整除,另外一层意思也就是说,B是A的一个因式,使这个因式B等于0的值,必是A的一个解.

练习册系列答案
相关题目
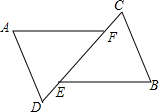 如图所示,△ADF和△BCE中,BE∥AF,点D,E,F,C在同-直线上,有如下三个关系式:①AD=BC;②DE=CF;③∠A=∠B.
如图所示,△ADF和△BCE中,BE∥AF,点D,E,F,C在同-直线上,有如下三个关系式:①AD=BC;②DE=CF;③∠A=∠B.