题目内容
17.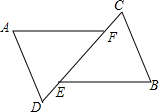 如图所示,△ADF和△BCE中,BE∥AF,点D,E,F,C在同-直线上,有如下三个关系式:①AD=BC;②DE=CF;③∠A=∠B.
如图所示,△ADF和△BCE中,BE∥AF,点D,E,F,C在同-直线上,有如下三个关系式:①AD=BC;②DE=CF;③∠A=∠B.(1)请用其中两个关系式作为条件,另一个作为结论,写出所有你认为正确的结论.
(2)选择(1)中你写出的一个正确结论,说明它正确的理由.
分析 (1)根据全等三角形的判断方法,可得:如果$\left\{\begin{array}{l}{AD=BC}\\{DE=CF}\end{array}\right.$,则∠A=∠B;如果$\left\{\begin{array}{l}{AD=BC}\\{∠A=∠B}\end{array}\right.$,则DE=CF;如果$\left\{\begin{array}{l}{DE=CF}\\{∠A=∠B}\end{array}\right.$,则AD=BC.
(2)根据全等三角形的判断方法,如果AD=BC,DE=CF,则DF=CE,再根据BE∥AF,判断出∠AFD=∠BEC,所以△AFD≌△BEC,∠A=∠B,据此解答即可.
解答 解:(1)根据全等三角形的判断方法,可得
如果$\left\{\begin{array}{l}{AD=BC}\\{DE=CF}\end{array}\right.$,则∠A=∠B;
如果$\left\{\begin{array}{l}{AD=BC}\\{∠A=∠B}\end{array}\right.$,则DE=CF;
如果$\left\{\begin{array}{l}{DE=CF}\\{∠A=∠B}\end{array}\right.$,则AD=BC.
(2)如果AD=BC,DE=CF,
则AD=BC,DF=CE,
∵BE∥AF,
∴∠AFD=∠BEC,
∴$\left\{\begin{array}{l}{AD=BC}\\{DF=CE}\\{∠AFD=∠BEC}\end{array}\right.$,
∴△AFD≌△BEC,
∴∠A=∠B,
即如果$\left\{\begin{array}{l}{AD=BC}\\{DE=CF}\end{array}\right.$,则∠A=∠B.
点评 此题主要考查了全等三角形的判断和性质,要熟练掌握,解答此题的关键是要明确:(1)在判定三角形全等时,关键是选择恰当的判定条件;(2)在应用全等三角形的判定时,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造三角形.

| A. | (a+1)2=a2+1 | B. | a2+a3=a5 | C. | a6÷a2=a3(a≠0) | D. | (-a2b)3=-a6b3 |
 已知:如图AE=AD,∠B=∠C,△ABD与△ACE全等吗?为什么?
已知:如图AE=AD,∠B=∠C,△ABD与△ACE全等吗?为什么?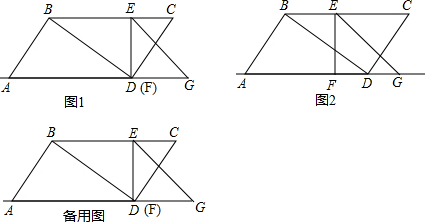
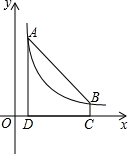 如图,点A(m,6)、B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.
如图,点A(m,6)、B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.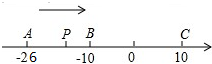 已知数轴上有A、B、C三点,分别表示有理数-26,-10,10,动点P从
已知数轴上有A、B、C三点,分别表示有理数-26,-10,10,动点P从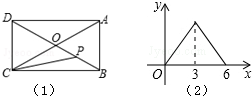 如图(1),矩形ABCD的两条对角线相交于点O,∠BOC=120°,AB=3,一动点P以均匀的速度沿折线OB-BA运动,若点P的运动时间x(s)与点C、O、P围成的三角形的面积y之间的函数图象如图(2),那么P点运动的速度为1.
如图(1),矩形ABCD的两条对角线相交于点O,∠BOC=120°,AB=3,一动点P以均匀的速度沿折线OB-BA运动,若点P的运动时间x(s)与点C、O、P围成的三角形的面积y之间的函数图象如图(2),那么P点运动的速度为1.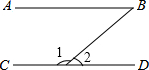 如图,AB∥CD,∠B+∠2=160°,则∠1=100°.
如图,AB∥CD,∠B+∠2=160°,则∠1=100°.