题目内容
2.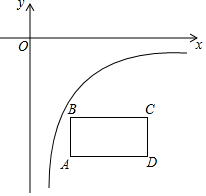 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象和矩形ABCD在第四象限,AD∥x轴,且AB=2,AD=4,点A的坐标为(2,-6).若将矩形向上平移,使矩形的两个顶点恰好同时落在反比例函数的图象上,则k的值是-6.
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象和矩形ABCD在第四象限,AD∥x轴,且AB=2,AD=4,点A的坐标为(2,-6).若将矩形向上平移,使矩形的两个顶点恰好同时落在反比例函数的图象上,则k的值是-6.
分析 根据反比例函数的图象性质及矩形的性质可知,平移后A、C落在反比例函数的图象上.设矩形平移后A的坐标是(2,-6+x),C的坐标是(6,-4+x),得出k=2(-6+x)=6(-4+x),求出x,即可得出矩形平移后A的坐标,代入反比例函数的解析式求出即可.
解答 解:设矩形平移后A的坐标是(2,-6+x),C的坐标是(6,-4+x),
∵A、C落在反比例函数的图象上,
∴k=2(-6+x)=6(-4+x),
解得x=3,
即矩形平移后A的坐标是(2,-3),
代入反比例函数的解析式得:k=2×(-3)=-6.
故答案为:-6.
点评 本题考查了矩形性质,反比例函数的图象性质,平移的性质的应用,主要考查学生的计算能力.

练习册系列答案
相关题目
11. 湖南省第二次文物普查时,省考古研究所在冷水滩钱家州征集到一个宋代“青釉瓜棱形瓷执壶”如图所示,该壶为盛酒器,瓷质,侈口,喇叭形长颈,长立把,则该“青釉瓜棱形瓷执壶”的主视图是( )
湖南省第二次文物普查时,省考古研究所在冷水滩钱家州征集到一个宋代“青釉瓜棱形瓷执壶”如图所示,该壶为盛酒器,瓷质,侈口,喇叭形长颈,长立把,则该“青釉瓜棱形瓷执壶”的主视图是( )
 湖南省第二次文物普查时,省考古研究所在冷水滩钱家州征集到一个宋代“青釉瓜棱形瓷执壶”如图所示,该壶为盛酒器,瓷质,侈口,喇叭形长颈,长立把,则该“青釉瓜棱形瓷执壶”的主视图是( )
湖南省第二次文物普查时,省考古研究所在冷水滩钱家州征集到一个宋代“青釉瓜棱形瓷执壶”如图所示,该壶为盛酒器,瓷质,侈口,喇叭形长颈,长立把,则该“青釉瓜棱形瓷执壶”的主视图是( )| A. | 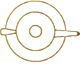 | B. | 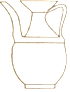 | C. |  | D. | 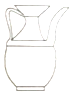 |
19.在二元一次方程:2x-3y=5中,用x表示y正确的是( )
| A. | 2x=5+3y | B. | 3y=5-2x | C. | x=$\frac{3y+5}{2}$ | D. | y=$\frac{2x-5}{3}$ |
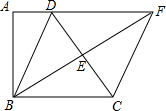 如图,四边形ABCD中,∠A=∠ABC=90°,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.
如图,四边形ABCD中,∠A=∠ABC=90°,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.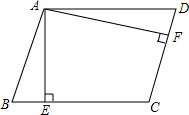 如图,平行四边形ABCD的邻边AD:AB=5:4,过点A作AE⊥BC,AF⊥CD,垂足分别为点E、F,AE=2cm,则AF=2.5cm.
如图,平行四边形ABCD的邻边AD:AB=5:4,过点A作AE⊥BC,AF⊥CD,垂足分别为点E、F,AE=2cm,则AF=2.5cm.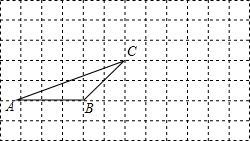 如图,在正方形网格中有一个格点三角形ABC,(即△ABC的各顶点都在格点上),按要求进行下列作图:
如图,在正方形网格中有一个格点三角形ABC,(即△ABC的各顶点都在格点上),按要求进行下列作图: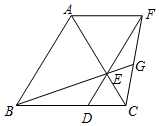 如图,点D,E在等边△ABC的边CB,CA上,且CD=CE,连接DE并延长到点F,使EF=AE,连接AF,CF,BE的延长线交CF于点G.
如图,点D,E在等边△ABC的边CB,CA上,且CD=CE,连接DE并延长到点F,使EF=AE,连接AF,CF,BE的延长线交CF于点G.