题目内容
14.解方程(1)4(x-8)=1+3(x+1)
(2)$\frac{3x-1}{2}$-1=$\frac{5x-7}{3}$.
分析 (1)先去括号,再移项,合并同类项即可;
(2)先去分母,再去括号,再移项,合并同类项,把x的系数化为1即可.
解答 解:(1)去括号得,4x-32=1+3x+3,
移项得,4x-3x=1+3+32,
合并同类项得,x=36;
(2)去分母得,3(3x-1)-6=2(5x-7)
去括号得,9x-3-6=10x-14,
移项得,9x-10x=-14+3+6,
合并同类项得,-x=-5,
把x的系数化为1得,x=5.
点评 本题考查的是解一元一次方程,去分母、去括号、移项、合并同类项、系数化为1,这仅是解一元一次方程的一般步骤,针对方程的特点,灵活应用,各种步骤都是为使方程逐渐向x=a形式转化.

练习册系列答案
相关题目
4.下列说法正确的个数是( )
①同一平面内,过一点有且只有一条直线与已知直线垂直;
②同一平面内,过一点有且只有一条直线与已知直线平行;
③若三条直线a⊥c,b⊥c,则a∥b;
④9的平方根是3;
⑤-2是4的平方根;
⑥平方根等于本身的数是0和1.
①同一平面内,过一点有且只有一条直线与已知直线垂直;
②同一平面内,过一点有且只有一条直线与已知直线平行;
③若三条直线a⊥c,b⊥c,则a∥b;
④9的平方根是3;
⑤-2是4的平方根;
⑥平方根等于本身的数是0和1.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
2.若把分式$\frac{2xy}{x+y}$(x,y为正数)中的x,y分别扩大为原来的3倍,则分式的值是( )
| A. | 扩大为原来的3倍 | B. | 缩小为原来的3倍 | C. | 扩大为原来的9倍 | D. | 不变 |
19. 为了解今年全县2000名初中学生“创新能力”大赛的笔试情况,随机抽取了部分同学的成绩,整理并制作如图所示图表,请你根据图表中信息,解答下列问题?
为了解今年全县2000名初中学生“创新能力”大赛的笔试情况,随机抽取了部分同学的成绩,整理并制作如图所示图表,请你根据图表中信息,解答下列问题?
(1)此次调查样本容量为300;
(2)在表中m=120; m=0.3;
(3)补全频数分布直方图.
 为了解今年全县2000名初中学生“创新能力”大赛的笔试情况,随机抽取了部分同学的成绩,整理并制作如图所示图表,请你根据图表中信息,解答下列问题?
为了解今年全县2000名初中学生“创新能力”大赛的笔试情况,随机抽取了部分同学的成绩,整理并制作如图所示图表,请你根据图表中信息,解答下列问题?| 分数段 | 步数 | 频率 |
| 60≤x<70 | 30 | 0.1 |
| 70≤x<80 | 90 | n |
| 80≤x<90 | m | 0.4 |
| 90≤x<100 | 60 | 0.2 |
(2)在表中m=120; m=0.3;
(3)补全频数分布直方图.
3.计算$\sqrt{9}$的算术平方根的相反数结果为( )
| A. | 3 | B. | -3 | C. | ±3 | D. | -$\sqrt{3}$ |
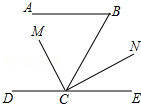 已知AB∥DE,∠B=68°,且CM平分∠DCB,CM⊥CN,垂足为C,求∠NCE的度数.
已知AB∥DE,∠B=68°,且CM平分∠DCB,CM⊥CN,垂足为C,求∠NCE的度数.
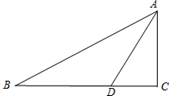 如图,已知在Rt△ABC中,∠C=90°,AD是∠BAC的角分线.
如图,已知在Rt△ABC中,∠C=90°,AD是∠BAC的角分线.