题目内容
11.下列各式中无论x为任何数都没有意义的是( )| A. | $\sqrt{-7x}$ | B. | $\sqrt{-199{9x}^{3}}$ | C. | $\sqrt{{-0.1x}^{2}-1}$ | D. | $\root{3}{-{6x}^{2}-5}$ |
分析 根据二次根式有意义的条件即可求出答案.
解答 解:(A)-7x≥0,
∴x≤0,故A不符合题意;
(B)-1999x3≥0,
∴x3≤0,
∴x≤0,故B不符合题意;
(C)-0.1x2-1≥0,
∴x2≤-10,此不等式对于任何实数都不能够成立,故C符合题意;
(D)-6x2-5只要是任何一个实数都可以成立,此时x可任意的值,故D不符合题意;
故选(C)
点评 本题考查二次根式有意义的条件,解题的关键是正确理解二次根式有意义的条件,本题属于基础题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.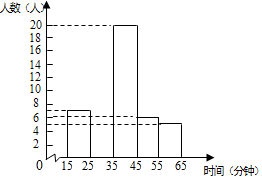 某校为了解学生平均每天课外阅读的时间,随机调查了该校部分学生一周内平均每天课外阅读的时间(以分钟为单位,并取整数),将有关数据统计整理并绘制成尚未完成的频率分布表和频数分布直方图.请你根据图表中所提供的信息,解答下列问题.
某校为了解学生平均每天课外阅读的时间,随机调查了该校部分学生一周内平均每天课外阅读的时间(以分钟为单位,并取整数),将有关数据统计整理并绘制成尚未完成的频率分布表和频数分布直方图.请你根据图表中所提供的信息,解答下列问题.
频率分布表
注:这里的15~25表示大于等于15同时小于25.
(1)求被调查的学生人数;
(2)直接写出频率分布表中的a和b的值,并补全频数分布直方图;
(3)若该校共有学生500名,则平均每天课外阅读的时间不少于35分钟的学生大约有多少名?
 某校为了解学生平均每天课外阅读的时间,随机调查了该校部分学生一周内平均每天课外阅读的时间(以分钟为单位,并取整数),将有关数据统计整理并绘制成尚未完成的频率分布表和频数分布直方图.请你根据图表中所提供的信息,解答下列问题.
某校为了解学生平均每天课外阅读的时间,随机调查了该校部分学生一周内平均每天课外阅读的时间(以分钟为单位,并取整数),将有关数据统计整理并绘制成尚未完成的频率分布表和频数分布直方图.请你根据图表中所提供的信息,解答下列问题.频率分布表
| 组别 | 分组 | 频数 | 频率 |
| 1 | 15~25 | 7 | 0.14 |
| 2 | 25~35 | a | 0.24 |
| 3 | 35~45 | 20 | 0.40 |
| 4 | 45~55 | 6 | b |
| 5 | 55~65 | 5 | 0.10 |
(1)求被调查的学生人数;
(2)直接写出频率分布表中的a和b的值,并补全频数分布直方图;
(3)若该校共有学生500名,则平均每天课外阅读的时间不少于35分钟的学生大约有多少名?
20.一辆汽车在公路上行驶,两次拐弯后,行驶的方向与原来的方向平行,则这两次拐弯的角度不可能是( )
| A. | 第一次向左拐40°,第二次向右拐40° | |
| B. | 第一次向右拐50°,第二次向左拐130° | |
| C. | 第一次向右拐60°,第二次向右拐120° | |
| D. | 第一次向左拐110°,第二次向右拐110° |
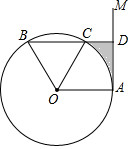 如图,点A是直线AM与⊙O的交点,点B在⊙O上,BD⊥AM垂足为D,BD与⊙O交于点C,OC平分∠AOB,∠B=60°.
如图,点A是直线AM与⊙O的交点,点B在⊙O上,BD⊥AM垂足为D,BD与⊙O交于点C,OC平分∠AOB,∠B=60°.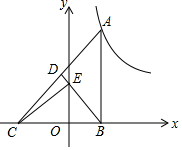 如图,Rt△ABC的直角边BC在x轴上,斜边AC上的中线BD交y轴于点E,双曲线y=$\frac{k}{x}$(k>0)的图象经过点A.若△BEC的面积为$\sqrt{6}$,则k的值为2$\sqrt{6}$.
如图,Rt△ABC的直角边BC在x轴上,斜边AC上的中线BD交y轴于点E,双曲线y=$\frac{k}{x}$(k>0)的图象经过点A.若△BEC的面积为$\sqrt{6}$,则k的值为2$\sqrt{6}$.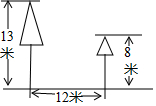 如图,校园内有两棵树,相距12米,一棵树高13米,另一棵树高8米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞13米.
如图,校园内有两棵树,相距12米,一棵树高13米,另一棵树高8米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞13米. 如图,矩形ABCD中,CE平分∠BCD,∠ACE=15°,则∠DOC,∠BOE的度数分别是30°和75°.
如图,矩形ABCD中,CE平分∠BCD,∠ACE=15°,则∠DOC,∠BOE的度数分别是30°和75°.