题目内容
16．
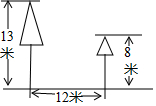如图，校园内有两棵树，相距12米，一棵树高13米，另一棵树高8米，一只小鸟从一棵树的顶端飞到另一棵树的顶端，小鸟至少要飞13米．
分析 根据“两点之间线段最短”可知：小鸟沿着两棵树的顶端进行直线飞行，所行的路程最短，运用勾股定理可将两点之间的距离求出．
解答 解：如图所示，AB，CD为树，且AB=13米，CD=8米，BD为两树距离12米，
过C作CE⊥AB于E，
则CE=BD=12AE=AB-CD=5，
在直角三角形AEC中，
斜边长AC=$\sqrt{C{E}^{2}+A{E}^{2}}$=13米，即小鸟至少要飞13米．
故答案为13．
点评 本题考查了勾股定理的应用，关键是从实际问题中构建出数学模型，转化为数学知识，然后利用直角三角形的性质解题．
练习册系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
单元加期末复习先锋大考卷系列答案
相关题目
12．7的绝对值是（ ）
| A． | -7 | B． | 7 | C． | $\frac{1}{7}$ | D． | $-\frac{1}{7}$ |
13．下列运算正确的是（ ）
| A． | 3x+2y=5（x+y） | B． | x+x3=x4 | C． | x2•x3=x6 | D． | （x2）3=x6 |
4．
如图，在矩形ABCD中，AB=4，BC=6，点E为BC的中点，将△ABE沿AE折叠，使点B落在矩形内点F处，连接CF，则CF的长为（ ）
如图，在矩形ABCD中，AB=4，BC=6，点E为BC的中点，将△ABE沿AE折叠，使点B落在矩形内点F处，连接CF，则CF的长为（ ）| A． | 1.8 | B． | 2.4 | C． | 3.2 | D． | 3.6 |
11．下列各式中无论x为任何数都没有意义的是（ ）
| A． | $\sqrt{-7x}$ | B． | $\sqrt{-199{9x}^{3}}$ | C． | $\sqrt{{-0.1x}^{2}-1}$ | D． | $\root{3}{-{6x}^{2}-5}$ |
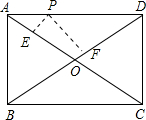如图，点P是矩形ABCD的边AD上的一动点，矩形的两条边AB、BC的长分别是6和8，则点P到矩形的两条对角线距离之和PE+PF是（ ）