题目内容
8.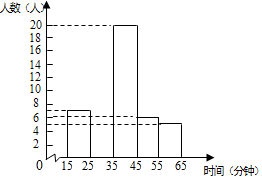 某校为了解学生平均每天课外阅读的时间,随机调查了该校部分学生一周内平均每天课外阅读的时间(以分钟为单位,并取整数),将有关数据统计整理并绘制成尚未完成的频率分布表和频数分布直方图.请你根据图表中所提供的信息,解答下列问题.
某校为了解学生平均每天课外阅读的时间,随机调查了该校部分学生一周内平均每天课外阅读的时间(以分钟为单位,并取整数),将有关数据统计整理并绘制成尚未完成的频率分布表和频数分布直方图.请你根据图表中所提供的信息,解答下列问题.频率分布表
| 组别 | 分组 | 频数 | 频率 |
| 1 | 15~25 | 7 | 0.14 |
| 2 | 25~35 | a | 0.24 |
| 3 | 35~45 | 20 | 0.40 |
| 4 | 45~55 | 6 | b |
| 5 | 55~65 | 5 | 0.10 |
(1)求被调查的学生人数;
(2)直接写出频率分布表中的a和b的值,并补全频数分布直方图;
(3)若该校共有学生500名,则平均每天课外阅读的时间不少于35分钟的学生大约有多少名?
分析 (1)根据第一组频数是7,频率是0.14即可求得被调查的人数;
(2)利用频率公式即可求得a和b的值,再补全频数分布直方图;
(3)利用总人数500乘以对应的频率即可求解.
解答 解:(1)被调查的人数是7÷0.14=50;
(2)a=50×0.24=12,b=$\frac{6}{50}$=0.12,
如图所示:
(3)平均每天课外阅读的时间不少于35分钟的学生大约有500×(0.40+0.12+0.10)=310(人).
点评 本题考查了频率分布直方图的知识,解题的关键是弄清频数、频率及样本容量的关系.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
18.一个扇形的弧长是10πcm,面积是60πcm2,则此扇形的圆心角的度数是( )
| A. | 300° | B. | 150° | C. | 120° | D. | 75° |
19.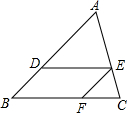 如图,在△ABC中,DE∥BC,∠ADE=∠EFC,AD:BD=5:3,CF=6,则DE的长为( )
如图,在△ABC中,DE∥BC,∠ADE=∠EFC,AD:BD=5:3,CF=6,则DE的长为( )
 如图,在△ABC中,DE∥BC,∠ADE=∠EFC,AD:BD=5:3,CF=6,则DE的长为( )
如图,在△ABC中,DE∥BC,∠ADE=∠EFC,AD:BD=5:3,CF=6,则DE的长为( )| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
13.下列运算正确的是( )
| A. | 3x+2y=5(x+y) | B. | x+x3=x4 | C. | x2•x3=x6 | D. | (x2)3=x6 |
11.下列各式中无论x为任何数都没有意义的是( )
| A. | $\sqrt{-7x}$ | B. | $\sqrt{-199{9x}^{3}}$ | C. | $\sqrt{{-0.1x}^{2}-1}$ | D. | $\root{3}{-{6x}^{2}-5}$ |