题目内容
 如图,平面内两条互相垂直的直线相交于点O,∠MON=90°,点A、B分别在射线OM、ON上移动,AC是△BAO的角平分线,BD为∠ABN的角平分线,AC与BD的反向延长线交于点P.试问:随着点A、B位置的变化,∠APB的大小是否会变化?若保持不变,请求出∠APB的度数;若发生变化,求出变化范围.
如图,平面内两条互相垂直的直线相交于点O,∠MON=90°,点A、B分别在射线OM、ON上移动,AC是△BAO的角平分线,BD为∠ABN的角平分线,AC与BD的反向延长线交于点P.试问:随着点A、B位置的变化,∠APB的大小是否会变化?若保持不变,请求出∠APB的度数;若发生变化,求出变化范围.考点:三角形内角和定理,三角形的外角性质
专题:
分析:根据角平分线的定义、三角形的内角和、外角性质求解.
解答:解:∠APB的大小保持不变.理由:
∵∠ABN=90°+∠OAB,AC平分∠OAB,BD平分∠ABN,
∴∠ABD=
∠ABN=
(90°+∠OAB)=45°+
∠OAB,
即∠ABD=45°+∠PAB,
又∵∠ABD=∠P+∠PAB,
∴∠APB=45°,
故∠APB的大小不发生变化,且始终保持45°.
∵∠ABN=90°+∠OAB,AC平分∠OAB,BD平分∠ABN,
∴∠ABD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即∠ABD=45°+∠PAB,
又∵∠ABD=∠P+∠PAB,
∴∠APB=45°,
故∠APB的大小不发生变化,且始终保持45°.
点评:本题考查的是三角形内角与外角的关系,解答此题目要注意:
①求角的度数常常要用到“三角形的内角和是180°”这一隐含的条件;
②三角形的外角通常情况下是转化为内角来解决.
①求角的度数常常要用到“三角形的内角和是180°”这一隐含的条件;
②三角形的外角通常情况下是转化为内角来解决.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
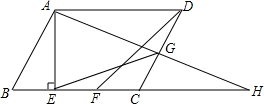 已知在平行四边形ABCD中,AE⊥BC,垂足为E,CE=CD,F为CE的中点,G为CD上的一点,连接DF、EG、AG,并延长AG、BC交于点H,∠DFC=∠EGC.
已知在平行四边形ABCD中,AE⊥BC,垂足为E,CE=CD,F为CE的中点,G为CD上的一点,连接DF、EG、AG,并延长AG、BC交于点H,∠DFC=∠EGC.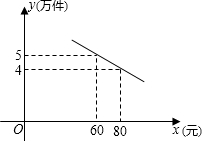 某商场销售一种市场需求较大的健身器材,已知每件产品的进价为40元,每年销售该种产品的总费用(不含进货费用)总计120万元.在销售过程中发现,年销售量y(万件)与销售单价x(元/件)之间存在着如图所示的一次函数关系.若商场希望该种产品一年的销售利润为40万元,请你为商场定一个销售单价.(年销售利润=年销售额-年销售产品进货总费用-年销售总费用)
某商场销售一种市场需求较大的健身器材,已知每件产品的进价为40元,每年销售该种产品的总费用(不含进货费用)总计120万元.在销售过程中发现,年销售量y(万件)与销售单价x(元/件)之间存在着如图所示的一次函数关系.若商场希望该种产品一年的销售利润为40万元,请你为商场定一个销售单价.(年销售利润=年销售额-年销售产品进货总费用-年销售总费用)