题目内容
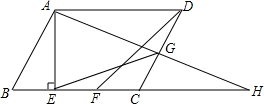 已知在平行四边形ABCD中,AE⊥BC,垂足为E,CE=CD,F为CE的中点,G为CD上的一点,连接DF、EG、AG,并延长AG、BC交于点H,∠DFC=∠EGC.
已知在平行四边形ABCD中,AE⊥BC,垂足为E,CE=CD,F为CE的中点,G为CD上的一点,连接DF、EG、AG,并延长AG、BC交于点H,∠DFC=∠EGC.(1)若CF=2,AE=3,求BE的长;
(2)求证:点G为CD中点;
(3)求证:∠AGE=2∠CEG.
考点:平行四边形的性质,全等三角形的判定与性质
专题:
分析:(1)求出DC=CE=2CF=4,求出AB,根据勾股定理求出BE即可;
(2)过G作GM⊥AE于M,证△DCF≌△ECG,推出CG=CF,求出M为AE中点,
(3)由(2)可得出等腰三角形AGE,根据性质得出GM是∠AGE的角平分线,即可得出答案.
(2)过G作GM⊥AE于M,证△DCF≌△ECG,推出CG=CF,求出M为AE中点,
(3)由(2)可得出等腰三角形AGE,根据性质得出GM是∠AGE的角平分线,即可得出答案.
解答:(1)解:∵CE=CD,点F为CE的中点,CF=2,
∴DC=CE=2CF=4,
∵四边形ABCD是平行四边形,
∴AB=CD=4,
∵AE⊥BC,
∴∠AEB=90°,
在Rt△ABE中,由勾股定理得:BE=
=
;
(2)证明:过G作GM⊥AE于M,
∵AE⊥BE,GM⊥AE,
∴GM∥BC∥AD,
∵在△DCF和△ECG中,
,
∴△DCF≌△ECG(AAS),
∴CG=CF,
∵CE=CD,CE=2CF,
∴CD=2CG,
即G为CD中点;
(3)∵AD∥GM∥BC,G为CD中点,
∴M为AE中点,
∴AM=EM,
∵GM⊥AE,
∴AG=EG,
∴∠AGM=∠EGM,
∴∠AGE=2∠MGE,
∵GM∥BC,
∴∠EGM=∠CEG,
∴∠AGE=2∠CEG.
∴DC=CE=2CF=4,
∵四边形ABCD是平行四边形,
∴AB=CD=4,
∵AE⊥BC,
∴∠AEB=90°,
在Rt△ABE中,由勾股定理得:BE=
| AB2-AE2 |
| 7 |
(2)证明:过G作GM⊥AE于M,
∵AE⊥BE,GM⊥AE,
∴GM∥BC∥AD,
∵在△DCF和△ECG中,
|
∴△DCF≌△ECG(AAS),

∴CG=CF,
∵CE=CD,CE=2CF,
∴CD=2CG,
即G为CD中点;
(3)∵AD∥GM∥BC,G为CD中点,
∴M为AE中点,
∴AM=EM,
∵GM⊥AE,
∴AG=EG,
∴∠AGM=∠EGM,
∴∠AGE=2∠MGE,
∵GM∥BC,
∴∠EGM=∠CEG,
∴∠AGE=2∠CEG.
点评:本题考查了平行四边形性质,等腰三角形的性质和判定,平行线分线段成比例定理,全等三角形的性质和判定,勾股定理等知识点的应用,主要考查学生综合运用定理进行推理的能力.

练习册系列答案
相关题目
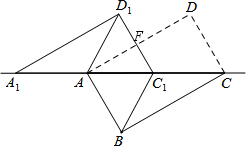 如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结AD1、BC1.若∠ACB=30°,AB=2,CC1=x,四边形ABC1D1的面积为S.
如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结AD1、BC1.若∠ACB=30°,AB=2,CC1=x,四边形ABC1D1的面积为S.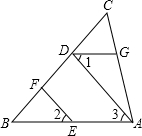 如图,EF∥AD,∠1=∠2,∠BAC=75°.求∠AGD的度数.
如图,EF∥AD,∠1=∠2,∠BAC=75°.求∠AGD的度数. 如图,平面内两条互相垂直的直线相交于点O,∠MON=90°,点A、B分别在射线OM、ON上移动,AC是△BAO的角平分线,BD为∠ABN的角平分线,AC与BD的反向延长线交于点P.试问:随着点A、B位置的变化,∠APB的大小是否会变化?若保持不变,请求出∠APB的度数;若发生变化,求出变化范围.
如图,平面内两条互相垂直的直线相交于点O,∠MON=90°,点A、B分别在射线OM、ON上移动,AC是△BAO的角平分线,BD为∠ABN的角平分线,AC与BD的反向延长线交于点P.试问:随着点A、B位置的变化,∠APB的大小是否会变化?若保持不变,请求出∠APB的度数;若发生变化,求出变化范围. 将矩形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C的坐标为(m,0)(m>0),点D(m,1)在BC上,将矩形OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E.
将矩形OABC置于平面直角坐标系中,点A的坐标为(0,4),点C的坐标为(m,0)(m>0),点D(m,1)在BC上,将矩形OABC沿AD折叠压平,使点B落在坐标平面内,设点B的对应点为点E. 如图,在△BOD中,OB=7,OD=3,将△BOD绕点O逆时针旋转90°至△AOC的位置,求图中阴影部分的面积.
如图,在△BOD中,OB=7,OD=3,将△BOD绕点O逆时针旋转90°至△AOC的位置,求图中阴影部分的面积. 如图,过点C(1,2)分别作x轴、y轴的平行线,交直线y=-x+4于A、B两点,若反比例函数y=
如图,过点C(1,2)分别作x轴、y轴的平行线,交直线y=-x+4于A、B两点,若反比例函数y=