题目内容
4.在平行四边形ABCD中,BC=3,∠ADC与∠BCD的平分线交线段AB于点E、点F,点E,点F恰好为线段AB的三等分点,求线段AB的长.分析 只要证明△AED、△BCF是等腰三角形即可解决问题.
解答 解:如图 ∵四边形ABCD是平行四边形,
∵四边形ABCD是平行四边形,
∴BC=AD=3,AB∥CD,
∴∠AED=∠EDC,∠BFC=∠DCF,
∵∠EDA=∠EDC,∠FCB=∠FCD,
∴∠AED=∠ADE,∠BFC=∠BCF,
∴AE=AD=3,BF=BC=3,
∵BE=EF=AF,
∴BE=EF=AF=1.5,
AB=BE+EF+AF=4.5.
点评 本题考查平行四边形的性质、角平分线的定义、等腰三角形的判定等知识,解题的关键是两个等腰三角形的发现,属于中考常考题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.若点P的坐标是(x,y),且满足x2+$\sqrt{y}$=0,则点P在( )
| A. | x轴的负半轴上 | B. | 第二象限 | C. | y轴的正半轴上 | D. | 坐标原点 |
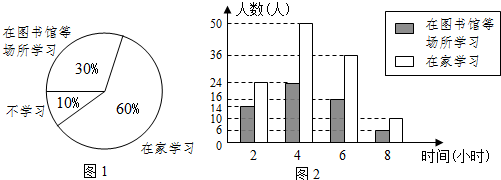
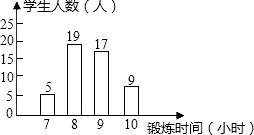 阳光体育运动,要求学生每一天锻炼一小时,如图是依据某班40名同学一周的体育锻炼时间绘制的条形统计图,那么关于该班50名同学一周参加体育锻炼时间的中位数为9小时.
阳光体育运动,要求学生每一天锻炼一小时,如图是依据某班40名同学一周的体育锻炼时间绘制的条形统计图,那么关于该班50名同学一周参加体育锻炼时间的中位数为9小时.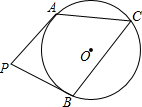 如图,PA,PB分别与⊙O相切于A,B两点,sin∠C=$\frac{4}{5}$,PA=$\frac{20}{3}$,则⊙O的面积为( )
如图,PA,PB分别与⊙O相切于A,B两点,sin∠C=$\frac{4}{5}$,PA=$\frac{20}{3}$,则⊙O的面积为( )