题目内容
3. 已知如图所示,四边形ABCD中,AB=6cm,AD=8cm,BC=26cm,CD=24cm,求四边形ABCD的面积.
已知如图所示,四边形ABCD中,AB=6cm,AD=8cm,BC=26cm,CD=24cm,求四边形ABCD的面积.
分析 连接BD,根据已知条件运用勾股定理逆定理可证△BCD为直角三角形,然后代入三角形面积公式将两直角三角形的面积求出来,两者面积相加即为四边形ABCD的面积.
解答 解:连接BD,
∵∠A=90°,
∴△ABD为直角三角形,
∵BD2=AB2+BD2=82+62=102,
∵AC>0,
∴BD=10,
在△BCD中,
∵DC2+BD2=100+576=676,BC2=262=676,
∴DC2+BD2=BC2,
∴△BCD为直角三角形,且∠BDC=90°,
∴S四边形ABCD=S△ABD+S△BCD=$\frac{1}{2}$×6×8+$\frac{1}{2}$×10×24=144.
点评 本题考查勾股定理、勾股定理等逆定理等知识,通过作辅助线可将一般的四边形转化为两个直角三角形是解题的关键.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
7.经过圆锥顶点的截面的形状可能是( )
| A. |  | B. |  | C. |  | D. |  |
12.农夫将苹果树种在正方形的果园内.为了保护苹果树不怕风吹,他在苹果树的周围种针叶树.在下图里,你可以看到农夫所种植苹果树的列数(n)和苹果树数量及针叶树数量的规律:当n为某一个数值时,苹果树数量会等于针叶树数量,则n为( )


| A. | 6 | B. | 8 | C. | 12 | D. | 16 |
13.用直尺和圆规作Rt△ABC斜边AB上的高线CD,甲、乙两人的作法如图:根据两人的作法可判断( )


| A. | 甲正确,乙错误 | B. | 乙正确,甲错误 | C. | 甲、乙均正确 | D. | 甲、乙均错误 |
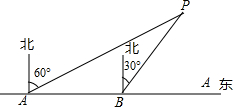 为了维护国家主权和海洋权利,海监部门对我国领海实现了常态化巡航管理,如图,正在执行巡航任务的海监船以每小时50海里的速度向正东方航行,在A处测得灯塔P在北偏东60°方向上,继续航行1小时到达B处,此时测得灯塔P在北偏东30°方向上.
为了维护国家主权和海洋权利,海监部门对我国领海实现了常态化巡航管理,如图,正在执行巡航任务的海监船以每小时50海里的速度向正东方航行,在A处测得灯塔P在北偏东60°方向上,继续航行1小时到达B处,此时测得灯塔P在北偏东30°方向上.


 如图,AB与CD相交于点E,AC∥DB,△ACE与△BDE是位似图形吗?
如图,AB与CD相交于点E,AC∥DB,△ACE与△BDE是位似图形吗?