题目内容
顺次连结对角线相等的四边形的四边中点所得图形是( )
| A、正方形 | B、矩形 |
| C、菱形 | D、以上都不对 |
考点:中点四边形
专题:
分析:作出图形,根据三角形的中位线平行于第三边并且等于第三边的一半可得EF=
AC,GH=
AC,HE=
BD,FG=
BD,再根据四边形的对角线相等可可知AC=BD,从而得到EF=FG=GH=HE,再根据四条边都相等的四边形是菱形即可得解.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:如图,E、F、G、H分别是四边形ABCD的边AB、BC、CD、DA的中点,
根据三角形的中位线定理,EF=
AC,GH=
AC,HE=
BD,FG=
BD,
连接AC、BD,
∵四边形ABCD的对角线相等,
∴AC=BD,
所以,EF=FG=GH=HE,
所以,四边形EFGH是菱形.
故选C.

根据三角形的中位线定理,EF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
连接AC、BD,
∵四边形ABCD的对角线相等,
∴AC=BD,
所以,EF=FG=GH=HE,
所以,四边形EFGH是菱形.
故选C.
点评:本题考查了菱形的判定和三角形的中位线的应用,熟记性质和判定定理是解此题的关键,注意:有四条边都相等的四边形是菱形.作图要注意形象直观.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
下列运算正确的是( )
A、-9÷2×
| ||||||
B、6÷(
| ||||||
C、1
| ||||||
D、-
|
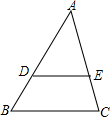 如图,在△ABC中,DE∥BC,DE分别与AB、AC相交于点D、E,若AD=4,AB=6,则DE:BC的值为( )
如图,在△ABC中,DE∥BC,DE分别与AB、AC相交于点D、E,若AD=4,AB=6,则DE:BC的值为( )A、
| ||
B、
| ||
C、
| ||
D、
|
从正面看、从左面看、从上面看都一样的几何体是( )
| A、圆柱 | B、长方体 | C、球 | D、五棱柱 |
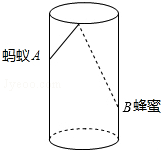 如图,圆柱形容器高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到达内壁B处的最短距离为
如图,圆柱形容器高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到达内壁B处的最短距离为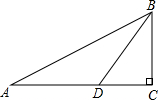 如图,在直角△ABC中,∠C=90°,点D在线段AC上,且∠A=30°,∠BDC=60°,AD=2,则BC=
如图,在直角△ABC中,∠C=90°,点D在线段AC上,且∠A=30°,∠BDC=60°,AD=2,则BC=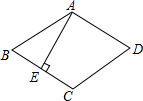 如图,在菱形ABCD中,∠C=120°,AE⊥BC于点E,求证:BE=CE.
如图,在菱形ABCD中,∠C=120°,AE⊥BC于点E,求证:BE=CE.