题目内容
12.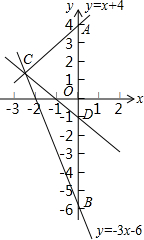 如图所示,设函数y=x+4的图象与y轴交于点A,函数y=-3x-6的图象与y轴交于点B,两个函数的图象交于点C,求通过线段AB的中点D及点C的一次函数表达式.
如图所示,设函数y=x+4的图象与y轴交于点A,函数y=-3x-6的图象与y轴交于点B,两个函数的图象交于点C,求通过线段AB的中点D及点C的一次函数表达式.
分析 根据题意可得出A(0,4)和B(0,-6),根据中点坐标公式可求出D的坐标,联立两解析式可求出C的坐标,运用待定系数法可求出函数解析式.
解答 解:由题意得:A的坐标为(0,4),B的坐标为(0,-6),
∴D的坐标为(0,-1),
联立两解析式可得:$\left\{\begin{array}{l}{y=x+4}\\{y=-3x-6}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=-\frac{5}{2}}\\{y=\frac{3}{2}}\end{array}\right.$,
∴C点坐标为(-$\frac{5}{2}$,$\frac{3}{2}$).
设通过线段AB的中点D及C点的一次函数的解析式为y=kx+b,
将点C和D的坐标代入得:$\left\{\begin{array}{l}{b=-1}\\{\frac{3}{2}=-\frac{5}{2}k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=-1}\end{array}\right.$,
故通过线段AB的中点D及C点的一次函数的表达式为y=-x-1.
点评 本题考查待定系数法求函数解析式,注意已知两点可以确定一个函数解析式,通过本题同学们要掌握待定系数法的运用.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
2.下列说法中正确的是( )
| A. | 正五边形是中心对称图形 | |
| B. | 平分弦的直径垂直于弦 | |
| C. | 化简-a$\sqrt{-\frac{1}{a}}$的结果是$\sqrt{-a}$ | |
| D. | 乘电梯从一楼到十楼共用时间20秒,则从一楼到五楼需用10秒 |
 如图,已知平面直角坐标系中A(-1,3),B(2,0),C(-3,-1).
如图,已知平面直角坐标系中A(-1,3),B(2,0),C(-3,-1). 如图,已知AD是△ABC的中线,AB=6,AC=4,△ACD的面积为6,那么△ABC的面积为12,△ABD与△ACD的周长之差是2,BC边的长可以为5(写出一个即可)
如图,已知AD是△ABC的中线,AB=6,AC=4,△ACD的面积为6,那么△ABC的面积为12,△ABD与△ACD的周长之差是2,BC边的长可以为5(写出一个即可)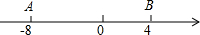 数轴上两个点A,B所对应的数为-8,4,A、B两点各自以一定的速度同时运动,且A点的运动速度为2个单位/秒.
数轴上两个点A,B所对应的数为-8,4,A、B两点各自以一定的速度同时运动,且A点的运动速度为2个单位/秒.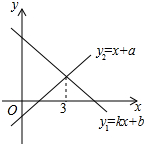 一次函数y1=kx+b与y2=x+a的图象如图所示,则下列结论:①k>0;②a>0;③当x<3时,y1<y2中,正确的个数是( )
一次函数y1=kx+b与y2=x+a的图象如图所示,则下列结论:①k>0;②a>0;③当x<3时,y1<y2中,正确的个数是( ) 如图,把Rt△ABC沿着直角边AC旋转1周,得到什么样的几何体?其中AC、BC在这个几何体中分别叫什么?
如图,把Rt△ABC沿着直角边AC旋转1周,得到什么样的几何体?其中AC、BC在这个几何体中分别叫什么?