题目内容
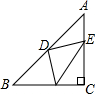 已知:如图所示Rt△ABC中,∠C=90°,AC=BC,D是AB中点,E、F分别是AC、BC边上的两动点,无论E、F如何运动,始终保持AE=CF.求证:△DEF是等腰直角三角形.
已知:如图所示Rt△ABC中,∠C=90°,AC=BC,D是AB中点,E、F分别是AC、BC边上的两动点,无论E、F如何运动,始终保持AE=CF.求证:△DEF是等腰直角三角形.考点:全等三角形的判定与性质,等腰直角三角形
专题:证明题
分析:连接CD,易证∠A=∠DCF=45°,AD=CD=BD,即可证明△ADE≌△CDF,可得DF=DE,∠CDF=∠ADE,即可求得∠EDF=90°,即可解题.
解答:证明:连接CD,

∵D是AB中点,Rt△ABC中,∠C=90°,AC=BC,
∴AD=CD=BD,
∠A=∠DCF=45°,∠ADC=90°,
在△ADE和△CDF中,
,
∴△ADE≌△CDF,(SAS)
∴DF=DE,∠CDF=∠ADE,
∵∠ADE+∠CDE=∠ADC=90°,
∴∠CDF+∠CDE=90°,即∠EDF=90°,
∴△DEF是等腰直角三角形.

∵D是AB中点,Rt△ABC中,∠C=90°,AC=BC,
∴AD=CD=BD,
∠A=∠DCF=45°,∠ADC=90°,
在△ADE和△CDF中,
|
∴△ADE≌△CDF,(SAS)
∴DF=DE,∠CDF=∠ADE,
∵∠ADE+∠CDE=∠ADC=90°,
∴∠CDF+∠CDE=90°,即∠EDF=90°,
∴△DEF是等腰直角三角形.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证△ADE≌△CDF是解题的关键.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
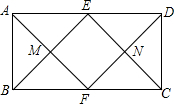 如图,在矩形ABCD中,E,F分别是AD,BC中点,连接AF,BE,CE,DF分别交于点M,N,四边形EMFN是( )
如图,在矩形ABCD中,E,F分别是AD,BC中点,连接AF,BE,CE,DF分别交于点M,N,四边形EMFN是( )| A、正方形 | B、菱形 |
| C、矩形 | D、无法确定 |
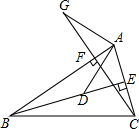 如图,BE,CF分别是△ABC的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AG,AD.求证:
如图,BE,CF分别是△ABC的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AG,AD.求证:
 如图,已知AB∥CD,AB=CD,BF=CE,求证:AE=DF.
如图,已知AB∥CD,AB=CD,BF=CE,求证:AE=DF. 某校体育老师为了解该校八年级学生对球类运动项目的喜爱情况,进行了随机抽样调查(每位学生必须且只能选择一项最喜爱的运动项目),并将调查结果进行整理,绘制了如图不完整的统计图表.请根据图表中的信息解答下列问题:
某校体育老师为了解该校八年级学生对球类运动项目的喜爱情况,进行了随机抽样调查(每位学生必须且只能选择一项最喜爱的运动项目),并将调查结果进行整理,绘制了如图不完整的统计图表.请根据图表中的信息解答下列问题: