题目内容
二次函数y=2x2+3x-5m的图象与x轴有交点,且交点在点(1,0)的左侧,求m的取值范围.
考点:抛物线与x轴的交点
专题:
分析:根据二次函数y=2x2+3x-5m的图象与x轴有交点,得到△≥0;根据交点在点(1,0)的左侧,得到结论:当x=1时,y>0;解不等式组即可解决问题.
解答:解:△=b2-4ac=32-4×2×(-5m)
=9+40m;对称轴方程x=-
=-
;
由题意得:
,
解得:-
≤m<1.
=9+40m;对称轴方程x=-
| 3 |
| 2×2 |
| 3 |
| 4 |
由题意得:
|
解得:-
| 9 |
| 40 |
点评:该题主要考查了抛物线与x轴的交点及其应用问题;解题的关键是根据题意,灵活运用抛物线的性质列出相应的方程或不等式,来分析、判断或解答.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
由一已知点P到圆上各点的最大距离为5,最小距离为1,则圆的半径为( )
| A、2或3 | B、3 |
| C、4 | D、2 或4 |
目前全球海洋面积约为36100万平方公里,用科学记数法将数36100万表示为( )
| A、3.61×108 |
| B、361×106 |
| C、3.61×104 |
| D、361×102 |
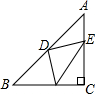 已知:如图所示Rt△ABC中,∠C=90°,AC=BC,D是AB中点,E、F分别是AC、BC边上的两动点,无论E、F如何运动,始终保持AE=CF.求证:△DEF是等腰直角三角形.
已知:如图所示Rt△ABC中,∠C=90°,AC=BC,D是AB中点,E、F分别是AC、BC边上的两动点,无论E、F如何运动,始终保持AE=CF.求证:△DEF是等腰直角三角形. 如图,在平面直角坐标系中,正方形OABC的顶点O为坐标原点,点B(0,6),反比例函数y=
如图,在平面直角坐标系中,正方形OABC的顶点O为坐标原点,点B(0,6),反比例函数y= 如图,矩形ABCD中,点M是CD的中点,点P是AB上的一动点,若AD=1,AB=2,则PA+PB+PM的最小值是
如图,矩形ABCD中,点M是CD的中点,点P是AB上的一动点,若AD=1,AB=2,则PA+PB+PM的最小值是