题目内容
 某校体育老师为了解该校八年级学生对球类运动项目的喜爱情况,进行了随机抽样调查(每位学生必须且只能选择一项最喜爱的运动项目),并将调查结果进行整理,绘制了如图不完整的统计图表.请根据图表中的信息解答下列问题:
某校体育老师为了解该校八年级学生对球类运动项目的喜爱情况,进行了随机抽样调查(每位学生必须且只能选择一项最喜爱的运动项目),并将调查结果进行整理,绘制了如图不完整的统计图表.请根据图表中的信息解答下列问题:| 类别 | 频数 |
| A.乒乓球 | 16 |
| B.足球 | 20 |
| C.排球 | n |
| D.篮球 | 15 |
| E.羽毛球 | m |
(2)若该年级有学生800人,请你估计这个年级最喜爱篮球的学生人数;
(3)在这次调查中随机抽中一名最喜爱足球的学生的概率是多少?
考点:频数(率)分布表,用样本估计总体,扇形统计图,概率公式
专题:
分析:(1)根据乒乓球的人数和所占的百分比求出总人数,再用总人数乘以羽毛球所占的百分比,求出m的值,再用总人数减去其它球类运动的人数,求出n的值;
(2)用总人数乘以最喜爱篮球的学生人数所占的百分比即可得出答案;
(3)根据概率公式即整体×样本的百分比,即可得出答案.
(2)用总人数乘以最喜爱篮球的学生人数所占的百分比即可得出答案;
(3)根据概率公式即整体×样本的百分比,即可得出答案.
解答:解:(1)调查的学生数是:
=80(人),
则m=80×21.25%=17(人),
n=80-16-20-15-17=12(人),
故答案为:17;12.
(2)根据题意得:
800×
=150(人),
答:估计这个年级有150人最喜爱篮球.
(3)∵喜爱足球的学生有20人,
∴在这次调查中随机抽中一名最喜爱足球的学生的概率是:P=
=
.
| 16 |
| 20% |
则m=80×21.25%=17(人),
n=80-16-20-15-17=12(人),
故答案为:17;12.
(2)根据题意得:
800×
| 15 |
| 80 |
答:估计这个年级有150人最喜爱篮球.
(3)∵喜爱足球的学生有20人,
∴在这次调查中随机抽中一名最喜爱足球的学生的概率是:P=
| 20 |
| 80 |
| 1 |
| 4 |
点评:此题考查了频率分布直方图,用到的知识点是频率=频数÷总数,用样本估计整体让整体×样本的百分比,读懂统计表,运用数形结合思想来解决由统计图形式给出的数学实际问题是本题的关键.

练习册系列答案
相关题目
函数y=x2-3x+4的图象与坐标轴的交点个数是( )
| A、0个 | B、1个 | C、2个 | D、3个 |
若a-|a|=2a,则实数a在数轴上的对应点一定在( )
| A、原点左侧 |
| B、原点或原点左侧 |
| C、原点右侧 |
| D、原点或原点右侧 |
-
的绝对值是( )
| 1 |
| 2 |
A、
| ||
B、-
| ||
| C、2 | ||
| D、-2 |
由一已知点P到圆上各点的最大距离为5,最小距离为1,则圆的半径为( )
| A、2或3 | B、3 |
| C、4 | D、2 或4 |
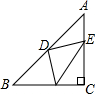 已知:如图所示Rt△ABC中,∠C=90°,AC=BC,D是AB中点,E、F分别是AC、BC边上的两动点,无论E、F如何运动,始终保持AE=CF.求证:△DEF是等腰直角三角形.
已知:如图所示Rt△ABC中,∠C=90°,AC=BC,D是AB中点,E、F分别是AC、BC边上的两动点,无论E、F如何运动,始终保持AE=CF.求证:△DEF是等腰直角三角形.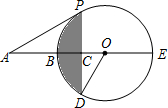 如图,BE是⊙O的直径,点A在EB的延长线上,弦PD⊥BE,垂足为C,连接OD,∠AOD=∠APC.
如图,BE是⊙O的直径,点A在EB的延长线上,弦PD⊥BE,垂足为C,连接OD,∠AOD=∠APC.