题目内容
13.计算:(1)(5m3n2)2×(-2m2)3×(-n2)4
(2)(-1)2014-(-$\frac{1}{3}$)-2×(π-3.14)0
(3)2a2+(a+b)(a-b)-(a-b)2
(4)[($\frac{x+y}{2}$)2-($\frac{x-y}{2}$)2]×(-$\frac{1}{2}$xy)
(5)若多项式x2+kxy+xy-2中不含xy项,且k2-(2a-1)=0,先化简再求(k+2a)2-(k-2a)2-2k(k-1)的值.
分析 (1)先计算积的乘方,然后利用单项式乘单项式的法则计算即可.
(2)根据正整数指数幂,负整数指数幂,零指数幂的定义计算即可.
(3)利用乘法公式展开,合并同类项即可.
(4)先利用平方差公式,再利用单项式乘单项式法则计算即可.
(5)先求出k、a的值,再利用乘法公式展开合并同类项,最后代入计算即可.
解答 解;(1)原式=25m6n4×(-8m6)×n8=-200m12n12.
(2)原式=1-9=-8.
(3)原式=2a2+a2-b2-(a2-2ab+b2)=2a2-2b2+2ab.
(4)原式=($\frac{x+y}{2}+\frac{x-y}{2}$)($\frac{x+y}{2}$-$\frac{x-y}{2}$)×(-$\frac{1}{2}$xy)
=xy×(-$\frac{1}{2}$xy)
=-$\frac{1}{2}$x2y2.
(5)由题意k+1=0,得k=-1,
∵且k2-(2a-1)=0,
∴a=1,
∴原式=k2+4ka+4a2-k2+4ka-4a2-2k2+2k=8ka-2k2+2k,
当k=-1,a=1时,原式=8×(-1)×1-2×(-1)2+2×(-1)=-12
点评 本题考查整式的混合运算,乘法公式,单项式乘单项式法则,多项式乘多项式法则等知识,解题的关键是灵活运用这些知识解决问题,注意符号问题,属于中考常考题型.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
4.在数轴上,原点左边的点表示的数是( )
| A. | 正数 | B. | 负数 | C. | 非正数 | D. | 非负数 |
1.下列计算中,不正确的是( )
| A. | 3$\sqrt{2}$×2$\sqrt{5}$=6$\sqrt{10}$ | B. | 3$\sqrt{6}$÷3$\sqrt{7}$=$\frac{6}{7}$ | C. | $\sqrt{2}$-5$\sqrt{2}$=-4$\sqrt{2}$ | D. | (3$\sqrt{2}$+2$\sqrt{3}$ )( 3$\sqrt{2}$-2$\sqrt{3}$)=6 |
2.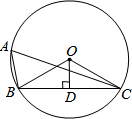 如图,⊙O的半径为2,点A为⊙O上一点,半径OD⊥弦BC于D,如果∠BAC=60°,那么OD的长是( )
如图,⊙O的半径为2,点A为⊙O上一点,半径OD⊥弦BC于D,如果∠BAC=60°,那么OD的长是( )
 如图,⊙O的半径为2,点A为⊙O上一点,半径OD⊥弦BC于D,如果∠BAC=60°,那么OD的长是( )
如图,⊙O的半径为2,点A为⊙O上一点,半径OD⊥弦BC于D,如果∠BAC=60°,那么OD的长是( )| A. | 2 | B. | $\sqrt{3}$ | C. | 1 | D. | $\frac{\sqrt{3}}{2}$ |
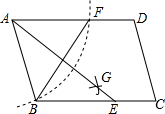 如图,在?ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=5,则AE的长为( )
如图,在?ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=5,则AE的长为( ) 如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,连接AC.若∠CAB=22.5°,CD=4cm,则⊙O的半径为2$\sqrt{2}$cm.
如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,连接AC.若∠CAB=22.5°,CD=4cm,则⊙O的半径为2$\sqrt{2}$cm.