题目内容
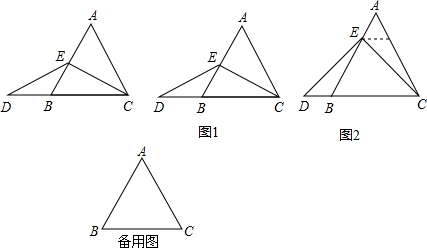
17. 已知∠ABC=90°,AB=BC,D为AC上的一点,分别过C点,A点作CE⊥BD于E点,AF⊥BD于F.若EC=5,EF=2,求AF的长.
已知∠ABC=90°,AB=BC,D为AC上的一点,分别过C点,A点作CE⊥BD于E点,AF⊥BD于F.若EC=5,EF=2,求AF的长.
分析 由CE⊥BD于E点,AF⊥BD于F,得出∠AFB=∠BEC=90°,再由∠1、∠2;∠3、∠2互余得出∠1=∠3,从而得出△AFB≌△BEC,由三角形全等的性质可得出AF=BE,BF=CE,结合EC=5,EF=2,即可得出结论.
解答 解: ∵CE⊥BD于E点,AF⊥BD于F,
∵CE⊥BD于E点,AF⊥BD于F,
∴∠AFB=∠BEC=90°,∠2+∠3=90°,
又∵∠1+∠2=90°,
∴∠1=∠3.
在△AFB和△BEC中,
$\left\{\begin{array}{l}{∠1=∠3}\\{∠AFB=∠BEC}\\{AB=BC}\end{array}\right.$,
∴△AFB≌△BEC(AAS).
∴AF=BE,BF=CE,
AF=BE=BF-EF=BE-EF=5-2=3.
点评 本题考查了全等三角形的判定及性质,解题的关键是找出△AFB≌△BEC.本题属于基础题,难度不大,解决该类型题目时,要去寻找相当的量,通过代换得出结论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12. 如图,在四边形ABCD中,已知∠ACB=∠BAD=105°,∠ABC=∠ADC=45°,则∠CAD的度数为( )
如图,在四边形ABCD中,已知∠ACB=∠BAD=105°,∠ABC=∠ADC=45°,则∠CAD的度数为( )
 如图,在四边形ABCD中,已知∠ACB=∠BAD=105°,∠ABC=∠ADC=45°,则∠CAD的度数为( )
如图,在四边形ABCD中,已知∠ACB=∠BAD=105°,∠ABC=∠ADC=45°,则∠CAD的度数为( )| A. | 60° | B. | 70° | C. | 75° | D. | 80° |
2.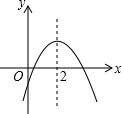 二次函数y=ax2+bx+c的图象如图所示,下列结论错误的是( )
二次函数y=ax2+bx+c的图象如图所示,下列结论错误的是( )
 二次函数y=ax2+bx+c的图象如图所示,下列结论错误的是( )
二次函数y=ax2+bx+c的图象如图所示,下列结论错误的是( )| A. | a<0 | B. | b>0 | ||
| C. | c<0 | D. | 当x>0时,y随x增大而增大 |
6.下列说法正确的是( )
| A. | 倒数等于它本身的数只有1 | B. | 相反数等于它本身的数只有1 | ||
| C. | 绝对值等于它本身的数是正数 | D. | 正数的绝对值是它本身 |
7.下列计算正确的是( )
| A. | (π-3)0=1 | B. | $\sqrt{18}$-$\sqrt{8}$=$\sqrt{10}$ | C. | (-4)-2=-$\frac{1}{16}$ | D. | $\sqrt{(-3)^{2}}$=-3 |