题目内容
8.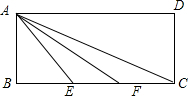 已知矩形ABCD,AB=BE=EF=FC=1,分别求出AE、AF、AC的长,并判断△AEF与△CEA是否相似?
已知矩形ABCD,AB=BE=EF=FC=1,分别求出AE、AF、AC的长,并判断△AEF与△CEA是否相似?
分析 先利用勾股定理计算出AE、AF、AC,再经过计算得到$\frac{AE}{EF}$=$\frac{EC}{AE}$,加上∠AEC=∠CEA,则根据两组对应边的比相等且夹角对应相等的两个三角形相似可判断△AEF∽△CEA.
解答 解:∵四边形ABCD为矩形,
∴∠B=90°,
在Rt△ABE中,AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
在Rt△ABF中,AF=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
在Rt△ABC中,AC=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
∵EF=1,EC=2,
∴$\frac{AE}{EF}$=$\sqrt{2}$,$\frac{EC}{AE}$=$\frac{2}{\sqrt{2}}$=$\sqrt{2}$,
∴$\frac{AE}{EF}$=$\frac{EC}{AE}$,
而∠AEC=∠CEA,
∴△AEF∽△CEA.
点评 本题考查了相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似.也考查了勾股定理.

练习册系列答案
相关题目
17.已知菱形ABCD,∠A等于120°,AB=6,E为AB的中点,F、M分别在AD、DC上滑动,且FM=3,则△FME面积的最大值为( ) 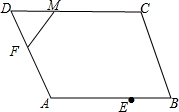

| A. | 12 | B. | 6 | C. | $\frac{7}{4}$$\sqrt{3}$ | D. | $\frac{9}{2}$$\sqrt{3}$ |
18.检验下列各方程的解正确的是( )
| A. | 2x-1=$\frac{2}{3}-3x(x=\frac{1}{3})$ | B. | 1=$\frac{x}{2}-4$(x=-10) | ||
| C. | 4x+2=-x-3(x=1) | D. | 0.48x-6=0.02x(x=1.2) |
 现有一块边长为a的正方形草坪,如图所示,将其相邻两边均扩大b,用两种方法计算扩大后草坪的面积.由此验证我们所学过的一个非常熟悉的公式,并写出这个公式.
现有一块边长为a的正方形草坪,如图所示,将其相邻两边均扩大b,用两种方法计算扩大后草坪的面积.由此验证我们所学过的一个非常熟悉的公式,并写出这个公式.