题目内容
17.已知菱形ABCD,∠A等于120°,AB=6,E为AB的中点,F、M分别在AD、DC上滑动,且FM=3,则△FME面积的最大值为( )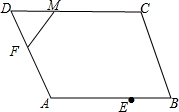
| A. | 12 | B. | 6 | C. | $\frac{7}{4}$$\sqrt{3}$ | D. | $\frac{9}{2}$$\sqrt{3}$ |
分析 找出CD的中点G,连接EG,可证得四边形AEGD是平行四边形,因为△FME在?AEGD中,三角形FME面积最大不会超过?AEGD面积的一半,又FM=3,所以当F与点D重合时,面积最大,最大为?AEGD面积的一半,由此得出答案即可.
解答 解:如图,
G为CD的中点,连接EG,
∵菱形ABCD,
∴AB∥CD,AB=BC=CD=DA,
∵E为AB的中点,G为CD的中点,
∴AE=GD=$\frac{1}{2}$AB=3,
∴四边形AEGD是平行四边形,
∵△FME在?AEGD中,
∴△FME面积最大不会超过?AEGD面积的一半,
∵FM=3,当F与点D重合时,面积最大,
∴△FME面积最大为?AEGD面积的一半,
∵∠A等于120°,AD=AB=6,作AH⊥CD垂足为点H,
∴∠D=60°,AH=6×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$,
∴△FME的最大面积=$\frac{1}{2}$×3×3$\sqrt{3}$=$\frac{9}{2}$$\sqrt{3}$.
故选:D.
点评 此题考查菱形的性质,平行四边形的判定与性质,三角形的面积,掌握在一个平行四边形中三角形的面积最大是所在平行四边形面积的一半是解决问题的根本.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
12.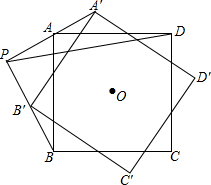 如图,点O是正方形ABCD中的对称中心,AB=2,将正方形ABCD绕点O旋转任意角度至正方形A′B′C′D′,直线AA′与直线BB′交于点P,则线段PD长度的最大值为( )
如图,点O是正方形ABCD中的对称中心,AB=2,将正方形ABCD绕点O旋转任意角度至正方形A′B′C′D′,直线AA′与直线BB′交于点P,则线段PD长度的最大值为( )
 如图,点O是正方形ABCD中的对称中心,AB=2,将正方形ABCD绕点O旋转任意角度至正方形A′B′C′D′,直线AA′与直线BB′交于点P,则线段PD长度的最大值为( )
如图,点O是正方形ABCD中的对称中心,AB=2,将正方形ABCD绕点O旋转任意角度至正方形A′B′C′D′,直线AA′与直线BB′交于点P,则线段PD长度的最大值为( )| A. | $\sqrt{5}$ | B. | 1 | C. | $\sqrt{5}$+1 | D. | $\sqrt{5}$-1 |
 如图,四边形ABCD中,∠B=∠D=90°,点E为AC的中点,则A,B,C,D四点共圆吗?
如图,四边形ABCD中,∠B=∠D=90°,点E为AC的中点,则A,B,C,D四点共圆吗?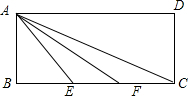 已知矩形ABCD,AB=BE=EF=FC=1,分别求出AE、AF、AC的长,并判断△AEF与△CEA是否相似?
已知矩形ABCD,AB=BE=EF=FC=1,分别求出AE、AF、AC的长,并判断△AEF与△CEA是否相似? 已知:△ABC中,ED∥BC,BD与CE交于点O,连接AO并延长交BC于点M,求证:M是BC中点.
已知:△ABC中,ED∥BC,BD与CE交于点O,连接AO并延长交BC于点M,求证:M是BC中点. 已知E为△ABC的AC边的中点,过E作FD,交AB于D,交BC的延长线于F.求证:AD•BF=BD•CF.
已知E为△ABC的AC边的中点,过E作FD,交AB于D,交BC的延长线于F.求证:AD•BF=BD•CF.