题目内容
已知,在△ABC中,∠BAC=90°,AB=AC,CE平分∠ACB交AB于点E.
(1)如图1,若点D在斜边BC上,DM垂直平分BE,垂足为M,求证:BD=AE;
(2)如图2,过点B作BF⊥CE,交CE的延长线于点F,若BF=2,求△BEC的面积.

(1)如图1,若点D在斜边BC上,DM垂直平分BE,垂足为M,求证:BD=AE;
(2)如图2,过点B作BF⊥CE,交CE的延长线于点F,若BF=2,求△BEC的面积.

考点:全等三角形的判定与性质,线段垂直平分线的性质,等腰直角三角形
专题:
分析:(1)连接DE,由∠BAC=90°,AB=AC,可得∠B=45°,由DM垂直平分BE,可得BD=DE,进而判断△BDE是等腰直角三角形,所以ED⊥BD,然后由角平分线的性质可得ED=AE,根据等量代换可得BD=AE;
(2)延长BF,CA,交与点G,由CE平分∠ACB,可得∠ACE=∠BCE,由BF⊥CE,可得∠BFC=∠GFC=90°,然后由三角形内角和定理可得:∠GBC=∠G,进而可得BC=GC,然后由等腰三角形的三线合一,可得BF=FG=
BG,所以BG=2BF=2FG=4,然后再由ASA,可证△ACE≌△ABG,可得EC=BG=4,最后根据三角形的面积公式即可求△BEC的面积.
(2)延长BF,CA,交与点G,由CE平分∠ACB,可得∠ACE=∠BCE,由BF⊥CE,可得∠BFC=∠GFC=90°,然后由三角形内角和定理可得:∠GBC=∠G,进而可得BC=GC,然后由等腰三角形的三线合一,可得BF=FG=
| 1 |
| 2 |
解答:解:(1)连接ED,如图1,
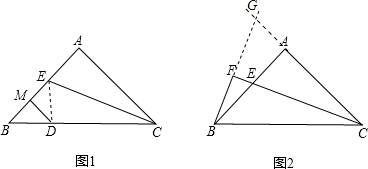
∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∵DM垂直平分BE,
∴BD=DE,
∴∠BED=∠EBD=45°,
∴∠EDC=∠EBD+∠BED=90°,
∵CE平分∠ACB,∠BAC=90°,∠EDC=90°,
∴ED=EA,
∴BD=AE;
(2)延长BF,CA,交与点G,如图2所示,

∵CE平分∠ACB,
∴∠ACE=∠BCE,
∵BF⊥CE,
∴∠BFC=∠GFC=90°,
∴∠GBC=∠G,
∴BC=GC,
∴BF=FG=
BG,
即BG=2BF=4,
∵∠GFC=∠GAB=90°,
∴∠ACF+∠BGC=90°,∠ABG+∠BGC=90°,
∴∠ACF=∠ABG,
在△ACE和△ABG中,
,
∴△ACE≌△ABG(SAS),
∴BG=CE,
∴EC=2BF=4,
∴S△ECB=
CE•BF=
×4×2=4.

∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∵DM垂直平分BE,
∴BD=DE,
∴∠BED=∠EBD=45°,
∴∠EDC=∠EBD+∠BED=90°,
∵CE平分∠ACB,∠BAC=90°,∠EDC=90°,
∴ED=EA,
∴BD=AE;
(2)延长BF,CA,交与点G,如图2所示,

∵CE平分∠ACB,
∴∠ACE=∠BCE,
∵BF⊥CE,
∴∠BFC=∠GFC=90°,
∴∠GBC=∠G,
∴BC=GC,
∴BF=FG=
| 1 |
| 2 |
即BG=2BF=4,
∵∠GFC=∠GAB=90°,
∴∠ACF+∠BGC=90°,∠ABG+∠BGC=90°,
∴∠ACF=∠ABG,
在△ACE和△ABG中,
|
∴△ACE≌△ABG(SAS),
∴BG=CE,
∴EC=2BF=4,
∴S△ECB=
| 1 |
| 2 |
| 1 |
| 2 |
点评:该题主要考查了全等三角形的判定及其性质的应用问题;准确找出命题中隐含的等量关系,是证明全等三角形的关键.

练习册系列答案
相关题目
国家提倡“低碳减排”,某公司计划建风能发电站,电站年均发电量约为258000000度,将数据258000000用科学记数法表示为( )
| A、258×106 |
| B、25.8×107 |
| C、2.58×108 |
| D、2.58×109 |
 如图,已知AB=AE,∠B=∠E,BC=ED,F是CD中点,说明AF⊥CD的理由.
如图,已知AB=AE,∠B=∠E,BC=ED,F是CD中点,说明AF⊥CD的理由. 如图,AB⊥AC,且AB=AC,BN⊥AN,CM⊥AN,若BN=3,CM=5,则MN=
如图,AB⊥AC,且AB=AC,BN⊥AN,CM⊥AN,若BN=3,CM=5,则MN= 如图,在等腰直角△ABC中,AC=BC,∠ACB=90°,D为BC的中点,DE⊥AB,垂足为E,过点B作BF∥AC交DE的延长线于点F,连CF,交AB于点G、交AD于点M,连DG.
如图,在等腰直角△ABC中,AC=BC,∠ACB=90°,D为BC的中点,DE⊥AB,垂足为E,过点B作BF∥AC交DE的延长线于点F,连CF,交AB于点G、交AD于点M,连DG.
 已知AB是⊙O的直径,弦CD⊥AB于点E,H是
已知AB是⊙O的直径,弦CD⊥AB于点E,H是