题目内容
探究题:如图:
(1)△ABC为等边三角形,动点D在边CA上,动点P边BC上,若这两点分别从C、B点同时出发,以相同的速度由C向A和由B向C运动,连接AP,BD交于点Q,两点运动过程中AP=BD成立吗?请证明你的结论;
(2)如果把原题中“动点D在边CA上,动点P边BC上,”改为“动点D,P在射线CA和射线BC上运动”,其他条
件不变,如图(2)所示,两点运动过程中∠BQP的大小保持不变.请你利用图(2)的情形,
求证:∠BQP=60°;
(3)如果把原题中“动点P在边BC上”改为“动点P在AB的延长线上运动,连接PD交BC于E”,其他条件不变,如图(3),则动点D,P在运动过程中,DE始终等于PE吗?写出证明过程.

(1)△ABC为等边三角形,动点D在边CA上,动点P边BC上,若这两点分别从C、B点同时出发,以相同的速度由C向A和由B向C运动,连接AP,BD交于点Q,两点运动过程中AP=BD成立吗?请证明你的结论;
(2)如果把原题中“动点D在边CA上,动点P边BC上,”改为“动点D,P在射线CA和射线BC上运动”,其他条
件不变,如图(2)所示,两点运动过程中∠BQP的大小保持不变.请你利用图(2)的情形,
求证:∠BQP=60°;
(3)如果把原题中“动点P在边BC上”改为“动点P在AB的延长线上运动,连接PD交BC于E”,其他条件不变,如图(3),则动点D,P在运动过程中,DE始终等于PE吗?写出证明过程.

考点:全等三角形的判定与性质,等边三角形的判定与性质
专题:
分析:(1)由△ABC为等边三角形,可得∠C=∠ABP=60°,AB=BC,又由这两点分别从C、B点同时出发,以相同的速度由C向A和由B向C运动,可得BP=CD,即可利用SAS,判定△ABP≌△BCD,继而证得结论;
(2)同理可证得△ABP≌△BCD(SAS),则可得∠APB=∠BDC,然后由∠APB-∠PAC=∠ACB=60°,∠DAQ=∠PAC,求得∠BDC-∠DAQ=∠BQP=60°;
(3)首先过点D作DG∥AB交BC于点G,则可证得△DCG为等边三角形,继而证得△DGE≌△PBE(AAS),则可证得结论.
(2)同理可证得△ABP≌△BCD(SAS),则可得∠APB=∠BDC,然后由∠APB-∠PAC=∠ACB=60°,∠DAQ=∠PAC,求得∠BDC-∠DAQ=∠BQP=60°;
(3)首先过点D作DG∥AB交BC于点G,则可证得△DCG为等边三角形,继而证得△DGE≌△PBE(AAS),则可证得结论.
解答:解:(1)成立.
理由:∵△ABC是等边三角形,
∴∠C=∠ABP=60°,AB=BC,
根据题意得:CD=BP,
在△ABP和△BCD中,
,
∴△ABP≌△BCD(SAS),
∴AP=BD;
(2)根据题意,CP=AD,
∴CP+BC=AD+AC,
即BP=CD,
在△ABP和△BCD中,
,
∴△ABP≌△BCD(SAS),
∴∠APB=∠BDC,
∵∠APB-∠PAC=∠ACB=60°,∠DAQ=∠PAC,
∴∠BDC-∠DAQ=∠BQP=60°;
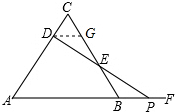 (2)DE=PE.
(2)DE=PE.
理由:过点D作DG∥AB交BC于点G,
∴∠CDG=∠C=∠CGD=60°,∠GDE=∠BPE,
∴△DCG为等边三角形,
∴DG=CD=BP,
在△DGE和△PBE中,
,
∴△DGE≌△PBE(AAS),
∴DE=PE.
理由:∵△ABC是等边三角形,
∴∠C=∠ABP=60°,AB=BC,
根据题意得:CD=BP,
在△ABP和△BCD中,
|
∴△ABP≌△BCD(SAS),
∴AP=BD;
(2)根据题意,CP=AD,
∴CP+BC=AD+AC,
即BP=CD,
在△ABP和△BCD中,
|
∴△ABP≌△BCD(SAS),
∴∠APB=∠BDC,
∵∠APB-∠PAC=∠ACB=60°,∠DAQ=∠PAC,
∴∠BDC-∠DAQ=∠BQP=60°;
 (2)DE=PE.
(2)DE=PE.理由:过点D作DG∥AB交BC于点G,
∴∠CDG=∠C=∠CGD=60°,∠GDE=∠BPE,
∴△DCG为等边三角形,
∴DG=CD=BP,
在△DGE和△PBE中,
|
∴△DGE≌△PBE(AAS),
∴DE=PE.
点评:此题考查了全等三角形的判定与性质以及等边三角形的性质.此题难度较大,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
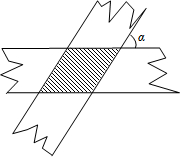 如图,两条宽度都为3cm的纸条,交叉重叠放在一起,它们的交角α为60°,则它们重叠部分(阴影部分)的面积为( )
如图,两条宽度都为3cm的纸条,交叉重叠放在一起,它们的交角α为60°,则它们重叠部分(阴影部分)的面积为( )A、2
| ||
B、3
| ||
C、4
| ||
D、6
|
 如图,已知PC是∠APB的平分线,点O是PB边上的一点,以O为圆心,OP长为半径画圆,⊙O分别交PA、PB、PC于A、B、C三点,过点C作CD⊥PA,垂足为D.
如图,已知PC是∠APB的平分线,点O是PB边上的一点,以O为圆心,OP长为半径画圆,⊙O分别交PA、PB、PC于A、B、C三点,过点C作CD⊥PA,垂足为D.
 在一次数学课上,王老师在黑板上画出如图,并写下了四个等式:①AB=DC;②BE=CE;③∠B=∠C;④∠BAE=∠CDE.
在一次数学课上,王老师在黑板上画出如图,并写下了四个等式:①AB=DC;②BE=CE;③∠B=∠C;④∠BAE=∠CDE.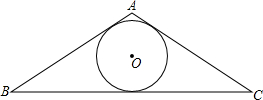 如图,已知△ABC的内切圆⊙O的半径为r,△ABC的周长为l,求△ABC的面积S.
如图,已知△ABC的内切圆⊙O的半径为r,△ABC的周长为l,求△ABC的面积S. 如图,点A,O,B在同一条直线上,∠COD=2∠COB,若∠COB=20°,则∠AOD的度数为
如图,点A,O,B在同一条直线上,∠COD=2∠COB,若∠COB=20°,则∠AOD的度数为