题目内容
为了探究n条直线能把平面最多分成几部分,我们从最简单的情形入手:
(1)一条直线把平面分成2部分;
(2)两条直线最多可把平面分成4部分;
(3)三条直线最多可把平面分成11部分…;
把上述探究的结果进行整理,列表分析:
(1)当直线条数为5时,把平面最多分成 部分,写成和的形式 ;
(2)当直线为n条时,把平面最多分成 部分.
(1)一条直线把平面分成2部分;
(2)两条直线最多可把平面分成4部分;
(3)三条直线最多可把平面分成11部分…;
把上述探究的结果进行整理,列表分析:
| 直线条数 | 把平面分成部分数 | 写成和形式 |
| 1 | 2 | 1+1 |
| 2 | 4 | 1+1+2 |
| 3 | 7 | 1+1+2+3 |
| 4 | 11 | 1+1+2+3+4 |
| … | … | … |
(2)当直线为n条时,把平面最多分成
考点:规律型:图形的变化类
专题:
分析:(1)根据表中规律,当直线条数为5时,把平面最多分成16部分,1+1+2+3+4+5=16;
(2)根据(1)的规律,得出当直线为n条时,把平面最多分成:1+1+2+3+…+n=1+
n(n+1).
(2)根据(1)的规律,得出当直线为n条时,把平面最多分成:1+1+2+3+…+n=1+
| 1 |
| 2 |
解答:解:(1)当直线条数为5时,把平面最多分成16部分,写成和的形式1+1+2+3+4+5;
(2)当直线为n条时,把平面最多分成1+
n(n+1)部分.
故答案为:16,1+2+3+4+5;1+
n(n+1).
(2)当直线为n条时,把平面最多分成1+
| 1 |
| 2 |
故答案为:16,1+2+3+4+5;1+
| 1 |
| 2 |
点评:此题考查图形的变化规律,从简单情形入手,找出一般的规律,利用规律解决问题.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
下列图形中,△A′B′C′与△ABC成轴对称的是( )
A、 |
B、 |
C、 |
D、 |
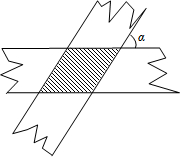 如图,两条宽度都为3cm的纸条,交叉重叠放在一起,它们的交角α为60°,则它们重叠部分(阴影部分)的面积为( )
如图,两条宽度都为3cm的纸条,交叉重叠放在一起,它们的交角α为60°,则它们重叠部分(阴影部分)的面积为( )A、2
| ||
B、3
| ||
C、4
| ||
D、6
|

 如图,点A,O,B在同一条直线上,∠COD=2∠COB,若∠COB=20°,则∠AOD的度数为
如图,点A,O,B在同一条直线上,∠COD=2∠COB,若∠COB=20°,则∠AOD的度数为 观察右面的图形(每个正方形的边长均为1)和左面相应的等式,探究其中的规律:那么第五个等式是
观察右面的图形(每个正方形的边长均为1)和左面相应的等式,探究其中的规律:那么第五个等式是