题目内容
 如图,已知AB=AE,∠B=∠E,BC=ED,F是CD中点,说明AF⊥CD的理由.
如图,已知AB=AE,∠B=∠E,BC=ED,F是CD中点,说明AF⊥CD的理由.解:联结
在△ABC和△AED中,
|
所以△ABC≌△AED
所以
所以△ACD是等腰三角形.
由F是CD的中点
得AF⊥CD
考点:全等三角形的判定与性质
专题:推理填空题
分析:连结AC、AD.先通过SAS证得△ABC≌△AED,再根据全等三角形的性质求得AC=AD,最后根据等腰三角形的三线合一的性质得出结论.
解答:解:连结AC、AD.
在△ABC和△AED中,
所以△ABC≌△AED (SAS),
所以AC=AD (全等三角形的对应边相等),
所以△ACD是等腰三角形.
又因为F是CD的中点 ( 已知 ),
所以AF⊥CD ( 等腰三角形的三线合一 ).
在△ABC和△AED中,
|
所以△ABC≌△AED (SAS),
所以AC=AD (全等三角形的对应边相等),
所以△ACD是等腰三角形.
又因为F是CD的中点 ( 已知 ),
所以AF⊥CD ( 等腰三角形的三线合一 ).
点评:本题考查了三角形全等的判定及性质;熟练掌握全等三角形的判定及性质,本题的关键是通过作辅助线,把问题转化为三角形全等来解决,这是一种很重要的方法,注意掌握应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列各组式子中:①4xyz和7xy;②0.5x2y和0.5xy2;③m2n和nm2,其中是同类项的是( )
| A、① | B、② | C、③ | D、①② |
用四舍五入法得到a的近似数是3.80,精确地说,这个数的范围是( )
| A、3.795≤a<3.805 |
| B、3.75≤a<3.85 |
| C、3.75<a<3.85 |
| D、3.795<a≤3.805 |
下列图形中,△A′B′C′与△ABC成轴对称的是( )
A、 |
B、 |
C、 |
D、 |
 图,在△ABC中,D是BC边上的中点,DE⊥BC交∠BAC的平分线于点E,EF⊥AB于F,EG⊥AC的延长线于G,请你猜想BF与CG的关系,并说明为什么.
图,在△ABC中,D是BC边上的中点,DE⊥BC交∠BAC的平分线于点E,EF⊥AB于F,EG⊥AC的延长线于G,请你猜想BF与CG的关系,并说明为什么. 如图,已知PC是∠APB的平分线,点O是PB边上的一点,以O为圆心,OP长为半径画圆,⊙O分别交PA、PB、PC于A、B、C三点,过点C作CD⊥PA,垂足为D.
如图,已知PC是∠APB的平分线,点O是PB边上的一点,以O为圆心,OP长为半径画圆,⊙O分别交PA、PB、PC于A、B、C三点,过点C作CD⊥PA,垂足为D.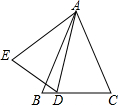 如图,已知在△ABC中,D为BC上的一点,AD平分∠EDC,且∠E=∠B,ED=DC.求证:AB=AC.
如图,已知在△ABC中,D为BC上的一点,AD平分∠EDC,且∠E=∠B,ED=DC.求证:AB=AC.
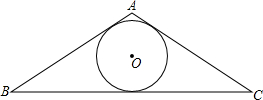 如图,已知△ABC的内切圆⊙O的半径为r,△ABC的周长为l,求△ABC的面积S.
如图,已知△ABC的内切圆⊙O的半径为r,△ABC的周长为l,求△ABC的面积S.