题目内容
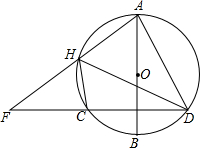 已知AB是⊙O的直径,弦CD⊥AB于点E,H是
已知AB是⊙O的直径,弦CD⊥AB于点E,H是 |
| AB |
考点:相似三角形的判定与性质,圆周角定理
专题:证明题
分析:先证明
=
,得出∠ADC=∠AHD,再由∠FHC=∠ADC,∠FCH=∠DAH,得出∠FHC=∠AHD,证出△AHD∽△CHF,即可证出AH:HC=AD:CF.
 |
| AC |
 |
| AD |
解答:证明:∵弦CD⊥AB,
∴
=
,
∴∠ADC=∠AHD,
∵∠FHC=∠ADC,∠FCH=∠DAH,
∴∠FHC=∠AHD,
∴△AHD∽△CHF,
∴AH:HC=AD:CF.
∴
 |
| AC |
 |
| AD |
∴∠ADC=∠AHD,
∵∠FHC=∠ADC,∠FCH=∠DAH,
∴∠FHC=∠AHD,
∴△AHD∽△CHF,
∴AH:HC=AD:CF.
点评:本题考查了圆周角定理和相似三角形的判定与性质;证明三角形相似是解决问题的关键.

练习册系列答案
相关题目
用四舍五入法得到a的近似数是3.80,精确地说,这个数的范围是( )
| A、3.795≤a<3.805 |
| B、3.75≤a<3.85 |
| C、3.75<a<3.85 |
| D、3.795<a≤3.805 |
下列图形中,△A′B′C′与△ABC成轴对称的是( )
A、 |
B、 |
C、 |
D、 |

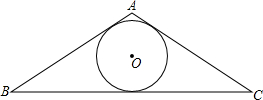 如图,已知△ABC的内切圆⊙O的半径为r,△ABC的周长为l,求△ABC的面积S.
如图,已知△ABC的内切圆⊙O的半径为r,△ABC的周长为l,求△ABC的面积S.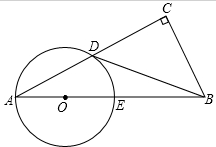 如图,在Rt△ABC中,∠C=90°,点D是AC上一点,过点A、D两点作⊙O.使圆心O在AB上,⊙O与AB交于点E,若BD为⊙O的切线,tan∠CBD=
如图,在Rt△ABC中,∠C=90°,点D是AC上一点,过点A、D两点作⊙O.使圆心O在AB上,⊙O与AB交于点E,若BD为⊙O的切线,tan∠CBD= 如图,点A,O,B在同一条直线上,∠COD=2∠COB,若∠COB=20°,则∠AOD的度数为
如图,点A,O,B在同一条直线上,∠COD=2∠COB,若∠COB=20°,则∠AOD的度数为