题目内容
已知二次函数C1:y=x2+(2m+1)x+m2的图象与y轴交于点C,顶点为D.
(1)若不论m为何值,二次函数C1图象的顶点D均在某一函数的图象上,直接写出此函数的解析式;
(2)若二次函数C1的图象与x轴的交点分别为M、N,设△MNC的外接圆的圆心为P.试说明⊙P与y轴的另一个交点Q为定点,并判断该定点Q是否在(1)中所求函数的图象上;
(3)当m=1时,将抛物线C1向下平移n(n>0)个单位,得到抛物线C2,直线DC与抛物线C2交于A、B两点,若AD+CB=DC,求n的值.
(1)若不论m为何值,二次函数C1图象的顶点D均在某一函数的图象上,直接写出此函数的解析式;
(2)若二次函数C1的图象与x轴的交点分别为M、N,设△MNC的外接圆的圆心为P.试说明⊙P与y轴的另一个交点Q为定点,并判断该定点Q是否在(1)中所求函数的图象上;
(3)当m=1时,将抛物线C1向下平移n(n>0)个单位,得到抛物线C2,直线DC与抛物线C2交于A、B两点,若AD+CB=DC,求n的值.

考点:二次函数综合题
专题:
分析:(1)利用题意得出函数顶点坐标,进而利用不论m为何值,二次函数C1图象的顶点D均在某一函数的图象上,得出k的值,进而得出答案;
(2)设M(x1,0),N(x2,0),点C的坐标为:(0,m2),则OM•ON=x1x2=m2,再利用切割线定理OM×ON=OC×OQ,进而得出OQ的值,即可得出Q点坐标;
(3)作AH⊥BH于点H,作DG⊥y轴于点G,得出m=1时,得出函数解析式,进而得出AB=2DC,AH=2DG=3,求出DC的解析式,进而利用根与系数关系得出n的值.
(2)设M(x1,0),N(x2,0),点C的坐标为:(0,m2),则OM•ON=x1x2=m2,再利用切割线定理OM×ON=OC×OQ,进而得出OQ的值,即可得出Q点坐标;
(3)作AH⊥BH于点H,作DG⊥y轴于点G,得出m=1时,得出函数解析式,进而得出AB=2DC,AH=2DG=3,求出DC的解析式,进而利用根与系数关系得出n的值.
解答: 解:(1)∵y=x2+(2m+1)x+m2=(x+m+
解:(1)∵y=x2+(2m+1)x+m2=(x+m+
)2-m-
,
若不论m为何值,二次函数C1图象的顶点D均在某一函数的图象上,
∴设函数解析式为:y=kx+b,
则-m-
=k(-m-
)+b,
故k=1,则b=
,
故此函数解析式为:y=x+
;
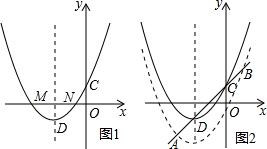
(2)如图1,设M(x1,0),N(x2,0),点C的坐标为:(0,m2),
则OM•ON=x1x2=m2,
设⊙P与y轴的另一个交点为Q,
OM×ON=OC×OQ,
则OQ=
=
=1,
∵m2>0,
∴点C在y轴的正半轴上,开口向上,从而点Q在y轴的正半轴上,
∴点Q为顶点,它的坐标为:(0,1),
Q(0,1)不在(1)中所求函数图象上;
(3)如图2,作AH⊥BH于点H,作DG⊥y轴于点G,
∵y=x2+(2m+1)x+m2中m=1,
∴y=x2+3x+1=(x+
)2-
,
则x=-
=-
,
∵AD+CB=DC,
∴AB=2DC,AH=2DG=3,
设抛物线C2的解析式为:y=x2+3x+1-n,
由题意可得:D(-
,-
),C(0,1),
设DC的解析式为:y=ax+c,则
,
解得:
故DC的解析式为:y=
x+1,
则x2+3x+1-n=
x+1,
故xA,xB是方程x2+
x-n=0两根,
xA+xB=-
,xAxB=-n,
故|xB-xA|=
,
则
=3,
解得:n=
.
 解:(1)∵y=x2+(2m+1)x+m2=(x+m+
解:(1)∵y=x2+(2m+1)x+m2=(x+m+| 1 |
| 2 |
| 1 |
| 4 |
若不论m为何值,二次函数C1图象的顶点D均在某一函数的图象上,
∴设函数解析式为:y=kx+b,
则-m-
| 1 |
| 4 |
| 1 |
| 2 |
故k=1,则b=
| 1 |
| 4 |
故此函数解析式为:y=x+
| 1 |
| 4 |
(2)如图1,设M(x1,0),N(x2,0),点C的坐标为:(0,m2),
则OM•ON=x1x2=m2,
设⊙P与y轴的另一个交点为Q,
OM×ON=OC×OQ,
则OQ=
| OM×ON |
| CO |
| |x1x2| |
| m2 |
∵m2>0,
∴点C在y轴的正半轴上,开口向上,从而点Q在y轴的正半轴上,
∴点Q为顶点,它的坐标为:(0,1),
Q(0,1)不在(1)中所求函数图象上;
(3)如图2,作AH⊥BH于点H,作DG⊥y轴于点G,
∵y=x2+(2m+1)x+m2中m=1,
∴y=x2+3x+1=(x+
| 3 |
| 2 |
| 5 |
| 4 |

则x=-
| b |
| 2a |
| 3 |
| 2 |
∵AD+CB=DC,
∴AB=2DC,AH=2DG=3,
设抛物线C2的解析式为:y=x2+3x+1-n,
由题意可得:D(-
| 3 |
| 2 |
| 5 |
| 4 |
设DC的解析式为:y=ax+c,则
|
解得:
|
故DC的解析式为:y=
| 3 |
| 2 |
则x2+3x+1-n=
| 3 |
| 2 |
故xA,xB是方程x2+
| 3 |
| 2 |
xA+xB=-
| 3 |
| 2 |
故|xB-xA|=
|
则
|
解得:n=
| 27 |
| 16 |
点评:此题主要考查了根与系数的关系以及待定系数法求一次函数解析式以及切割线定理等知识,熟练结合切割线定理得出QO的长是解题关键.

练习册系列答案
相关题目
 某学校为了解学生大课间体育活动情况,随机抽取本校100名学生进行调查.整理收集到的数据,绘制成如图的统计图.若该校共有800名学生,估计喜欢“踢毽子”的学生有( )人.
某学校为了解学生大课间体育活动情况,随机抽取本校100名学生进行调查.整理收集到的数据,绘制成如图的统计图.若该校共有800名学生,估计喜欢“踢毽子”的学生有( )人.| A、100 | B、200 |
| C、300 | D、400 |

 已知四边形ABCD外接⊙O的半径为10,对角线AC与BD的交点为E,且AB2=AE•AC,BD=16.
已知四边形ABCD外接⊙O的半径为10,对角线AC与BD的交点为E,且AB2=AE•AC,BD=16. 图中△ABE和△ACD都是等边三角形.△AEC和△ABD全等吗?如果要△ABE和△ACD全等,则还需要什么条件?
图中△ABE和△ACD都是等边三角形.△AEC和△ABD全等吗?如果要△ABE和△ACD全等,则还需要什么条件? 如图,正方形ABCD中,E、F分别在AD、DC上,EF的延长线交BC的延长线于G点,且∠AEB=∠BEG;
如图,正方形ABCD中,E、F分别在AD、DC上,EF的延长线交BC的延长线于G点,且∠AEB=∠BEG;