题目内容
 如图,正方形ABCD中,E、F分别在AD、DC上,EF的延长线交BC的延长线于G点,且∠AEB=∠BEG;
如图,正方形ABCD中,E、F分别在AD、DC上,EF的延长线交BC的延长线于G点,且∠AEB=∠BEG;(1)求证:∠ABE=
| 1 |
| 2 |
(2)若AB=4,AE=1,求S△BEG;
(3)若E、F两点分别在AD、DC上运动,其它条件不变,试问:线段AE、EF、FC三者之间是否存在确定的数量关系?若存在,请写出它们之间的数量关系,并证明;若不存在,请说明理由.
考点:四边形综合题
专题:综合题
分析:(1)由正方形的性质得AD∥BC,则∠AEB=∠GBE,由于∠AEB=∠BEG,根据等量代换得到∠BEG=∠GBE,根据三角形内角和定理得∠BGE=180°-∠BEG-∠EBG,所以
∠BGE=90°-∠BEG=90°-∠AEB,加上∠ABE=90°-∠AEB,所以∠ABE=
∠BGE;
(2)作GH⊥BE于H,如图1,在Rt△ABE中,利用勾股定理计算出BE=
,由△GBE为等腰三角形得BH=EH,则BH=
BE=
,再证明Rt△ABE∽Rt△BGH,利用相似比计算出GH=2
,然后根据三角形面积公式计算S△BEG;
(3)作BQ⊥GE于Q,如图2,先根据“AAS”证明BEA≌△BEQ,则AB=QB,AE=QE,则BQ=BC,再利用“HL”证明△BFQ≌△BFC,则FQ=FC,所以EF=EQ+FQ=AE+CF.
| 1 |
| 2 |
| 1 |
| 2 |
(2)作GH⊥BE于H,如图1,在Rt△ABE中,利用勾股定理计算出BE=
| 17 |
| 1 |
| 2 |
| ||
| 2 |
| 17 |
(3)作BQ⊥GE于Q,如图2,先根据“AAS”证明BEA≌△BEQ,则AB=QB,AE=QE,则BQ=BC,再利用“HL”证明△BFQ≌△BFC,则FQ=FC,所以EF=EQ+FQ=AE+CF.
解答:(1)证明:∵四边形ABCD为正方形,
∴AD∥BC,
∴∠AEB=∠GBE,
∵∠AEB=∠BEG,
∴∠BEG=∠GBE,
∴△GBE为等腰三角形,
∴∠BGE=180°-∠BEG-∠EBG,即∠BGE=180°-2∠BEG,
∴
∠BGE=90°-∠BEG=90°-∠AEB,
而∠ABE=90°-∠AEB,
∴∠ABE=
∠BGE;
(2)解:作GH⊥BE于H,如图1,
在Rt△ABE中,AB=4,AE=1,BE=
=
∵△GBE为等腰三角形,
∴BH=EH,
∴BH=
BE=
,
∵∠AEB=∠GBH,
∴Rt△ABE∽Rt△BGH,
∴
=
,即
=
,
∴GH=2
,
∴S△BEG=
×BE×GE=
×
×2
=17;
(3)解:AE+GF=EF.理由如下:
作BQ⊥GE于Q,如图2,
在△BEA和△BEQ中
,
∴△BEA≌△BEQ(AAS),
∴AB=QB,AE=QE,
而AB=BC,
∴BQ=BC,
在△BFQ和△BFC中
,
∴△BFQ≌△BFC(HL),
∴FQ=FC,
∴EF=EQ+FQ=AE+CF.
∴AD∥BC,
∴∠AEB=∠GBE,
∵∠AEB=∠BEG,
∴∠BEG=∠GBE,
∴△GBE为等腰三角形,
∴∠BGE=180°-∠BEG-∠EBG,即∠BGE=180°-2∠BEG,
∴
| 1 |
| 2 |
而∠ABE=90°-∠AEB,

∴∠ABE=
| 1 |
| 2 |
(2)解:作GH⊥BE于H,如图1,
在Rt△ABE中,AB=4,AE=1,BE=
| AB2+AE2 |
| 17 |
∵△GBE为等腰三角形,
∴BH=EH,
∴BH=
| 1 |
| 2 |
| ||
| 2 |
∵∠AEB=∠GBH,
∴Rt△ABE∽Rt△BGH,

∴
| AB |
| GH |
| AE |
| BH |
| 4 |
| GH |
| 1 | ||||
|
∴GH=2
| 17 |
∴S△BEG=
| 1 |
| 2 |
| 1 |
| 2 |
| 17 |
| 17 |
(3)解:AE+GF=EF.理由如下:
作BQ⊥GE于Q,如图2,
在△BEA和△BEQ中
|
∴△BEA≌△BEQ(AAS),
∴AB=QB,AE=QE,
而AB=BC,
∴BQ=BC,
在△BFQ和△BFC中
|
∴△BFQ≌△BFC(HL),
∴FQ=FC,
∴EF=EQ+FQ=AE+CF.
点评:本题考查了四边形的综合题:熟练掌握正方形的性质、等腰三角形的性质和全等三角形的判定与性质;会利用勾股定理和相似比进行几何计算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
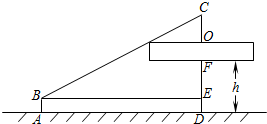 如图,一桥梁建设工地上有一架吊车,底座高AB=1.5米,吊臂长BC=18米,它与地面保持成30°角,现要将一个底面圆直径为8米,高为2米的圆柱体的钢筋混凝土框架,安装到离地面高度为6米的桥基上,问这架吊车能否完成这安装任务?请说明理由.(说明:图中钢索CO吊在长方体框架的上底面的中心处)
如图,一桥梁建设工地上有一架吊车,底座高AB=1.5米,吊臂长BC=18米,它与地面保持成30°角,现要将一个底面圆直径为8米,高为2米的圆柱体的钢筋混凝土框架,安装到离地面高度为6米的桥基上,问这架吊车能否完成这安装任务?请说明理由.(说明:图中钢索CO吊在长方体框架的上底面的中心处)