题目内容
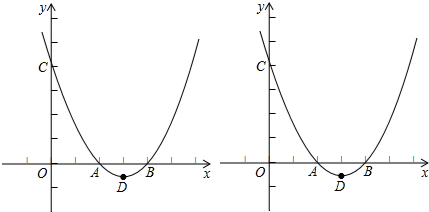
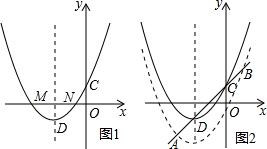
已知:如图,抛物线y=ax2-3x+c与x轴交于A、B,与y轴交于C,抛物线的顶点为D,D点的横坐标为3,C点的坐标为(0,4).
(1)求抛物线的解析式;
(2)P点从C点出发沿y轴负方向运动,Q点从B点出发沿x轴正方向运动,P、Q两点同时出发,速度均为每秒1个单位长度,过P点作x轴的平行线交抛物线于E,设运动时间为t(秒),当t为何值时,P、A、Q、E四点构成平行四边形;
(3)将抛物线向上平移2个单位长度,平移后的抛物线的顶点为F,交y轴于N,在平移后的抛物线上是否存在点M,使S△MNC=2S△MFD?若存在求出M点的坐标;若不存在,请说明理由.
(1)求抛物线的解析式;
(2)P点从C点出发沿y轴负方向运动,Q点从B点出发沿x轴正方向运动,P、Q两点同时出发,速度均为每秒1个单位长度,过P点作x轴的平行线交抛物线于E,设运动时间为t(秒),当t为何值时,P、A、Q、E四点构成平行四边形;
(3)将抛物线向上平移2个单位长度,平移后的抛物线的顶点为F,交y轴于N,在平移后的抛物线上是否存在点M,使S△MNC=2S△MFD?若存在求出M点的坐标;若不存在,请说明理由.

考点:二次函数综合题,解一元二次方程-直接开平方法,解一元二次方程-因式分解法,待定系数法求二次函数解析式,平行四边形的判定
专题:综合题
分析:(1)由条件可建立关于a与c的方程组,解这个方程组就可求出抛物线的解析式.
(2)由于PE∥AQ,只需PE=AQ,四边形APEQ就是平行四边形,此时PE=AQ=2+t,就可得到点E(2+t,4-t),代入抛物线的解析式就可求出t.
(3)设点M的坐标为(m,n),根据条件就可建立关于m的方程,解这个方程就可得到m,代入新抛物线的解析式就可求出点M的坐标.
(2)由于PE∥AQ,只需PE=AQ,四边形APEQ就是平行四边形,此时PE=AQ=2+t,就可得到点E(2+t,4-t),代入抛物线的解析式就可求出t.
(3)设点M的坐标为(m,n),根据条件就可建立关于m的方程,解这个方程就可得到m,代入新抛物线的解析式就可求出点M的坐标.
解答:解:(1)由题可得:
.
解得:
.
∴抛物线的解析式为y=
x2-3x+4.
(2)如图1,
由题可得:PE∥AQ,CP=BQ=t.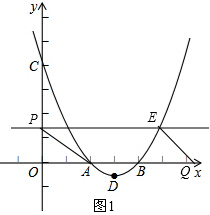
解方程
x2-3x+4=0得:x1=2,x2=4.
则点A(2,0),B(4,0).AB=2.
当PE=AQ时,四边形PAQE是平行四边形,
此时PE=AQ=AB+BQ=2+t.
则点E的坐标为(2+t,4-t).
∵点E在抛物线y=
x2-3x+4上,
∴
(2+t)2-3(2+t)+4=4-t.
解得:t1=2
,t2=-2
(舍去).
∴当t=2
秒时,P、A、Q、E四点构成平行四边形.
(3)存在.
由题可得:平移后的抛物线的解析式为y=
x2-3x+4+2=
x2-3x+6,且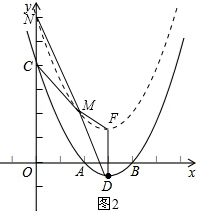 CN=DF=2.如图2,
CN=DF=2.如图2,
设点M的坐标为(m.n).
∵S△MNC=2S△MFD,
S△MNC=
×2×
=
,
S△MFD=
×2×
=
,
∴
=2
.
∴m2=4(3-m)2.
解得:m1=2,m2=6.
当m=2时,n=
×22-3×2+6=2,点M(2,2);
当m=6时,n=
×62-3×6+6=6,点M(6,6).
∴点M的坐标为(2,2)或(6,6).
|
解得:
|
∴抛物线的解析式为y=
| 1 |
| 2 |
(2)如图1,
由题可得:PE∥AQ,CP=BQ=t.

解方程
| 1 |
| 2 |
则点A(2,0),B(4,0).AB=2.
当PE=AQ时,四边形PAQE是平行四边形,
此时PE=AQ=AB+BQ=2+t.
则点E的坐标为(2+t,4-t).
∵点E在抛物线y=
| 1 |
| 2 |
∴
| 1 |
| 2 |
解得:t1=2
| 2 |
| 2 |
∴当t=2
| 2 |
(3)存在.
由题可得:平移后的抛物线的解析式为y=
| 1 |
| 2 |
| 1 |
| 2 |
 CN=DF=2.如图2,
CN=DF=2.如图2,设点M的坐标为(m.n).
∵S△MNC=2S△MFD,
S△MNC=
| 1 |
| 2 |
|
|
S△MFD=
| 1 |
| 2 |
|
|
∴
|
|
∴m2=4(3-m)2.
解得:m1=2,m2=6.
当m=2时,n=
| 1 |
| 2 |
当m=6时,n=
| 1 |
| 2 |
∴点M的坐标为(2,2)或(6,6).
点评:本题考查了用待定系数法求二次函数的解析式、解一元二次方程、平行四边形的判定等知识,有一定的综合性.需要注意的是:用坐标表示线段的长度时要加绝对值.

练习册系列答案
相关题目
 如图,与∠B是同旁内角的有( )
如图,与∠B是同旁内角的有( )| A、3个 | B、2个 | C、1个 | D、4个 |
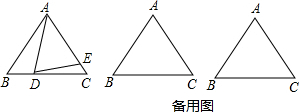
 如图,△ABC中,∠ABC=60°,AD,CE分别为BC,AB边上的高,
如图,△ABC中,∠ABC=60°,AD,CE分别为BC,AB边上的高,
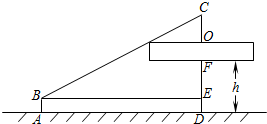 如图,一桥梁建设工地上有一架吊车,底座高AB=1.5米,吊臂长BC=18米,它与地面保持成30°角,现要将一个底面圆直径为8米,高为2米的圆柱体的钢筋混凝土框架,安装到离地面高度为6米的桥基上,问这架吊车能否完成这安装任务?请说明理由.(说明:图中钢索CO吊在长方体框架的上底面的中心处)
如图,一桥梁建设工地上有一架吊车,底座高AB=1.5米,吊臂长BC=18米,它与地面保持成30°角,现要将一个底面圆直径为8米,高为2米的圆柱体的钢筋混凝土框架,安装到离地面高度为6米的桥基上,问这架吊车能否完成这安装任务?请说明理由.(说明:图中钢索CO吊在长方体框架的上底面的中心处)