题目内容
10.(1)解方程:x2-4x+1=0(配方法)(2)解不等式组:$\left\{\begin{array}{l}{1-3x≤5-x}\\{4-5x>-x}\end{array}\right.$.
分析 (1)首先把1移到等号右边,然后再两边同时加上4,可得(x-2)2=3,然后再两边同时开平方即可;
(2)首先分别计算出两个不等式的解集,再根据大小小大中间找确定不等式组的解集.
解答 解:(1)x2-4x=-1,
x2-4x+4=-1+4,
(x-2)2=3,
x-2=±$\sqrt{3}$,
则x-2=-$\sqrt{3}$,x-2=$\sqrt{3}$,
x1=$-\sqrt{3}$+2,x2=$\sqrt{3}+2$.
(2)$\left\{\begin{array}{l}{1-3x≤5-x①}\\{4-5x>-x②}\end{array}\right.$,
由①得:x≥-2,
由②得:x<1,
不等式组的解集为:-2≤x<1.
点评 此题主要考查了一元二次方程和一元一次不等式的解法,关键是掌握解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
20.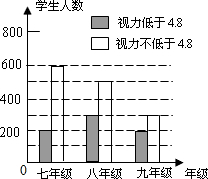 某学习小组对所在城区初中学生的视力情况进行抽样调查,如图是这些同学根据调查结果画出的条形统计图如图所示,则下列说法中不正确的是( )
某学习小组对所在城区初中学生的视力情况进行抽样调查,如图是这些同学根据调查结果画出的条形统计图如图所示,则下列说法中不正确的是( )
 某学习小组对所在城区初中学生的视力情况进行抽样调查,如图是这些同学根据调查结果画出的条形统计图如图所示,则下列说法中不正确的是( )
某学习小组对所在城区初中学生的视力情况进行抽样调查,如图是这些同学根据调查结果画出的条形统计图如图所示,则下列说法中不正确的是( )| A. | 本次抽查活动共抽查了2100名学生 | |
| B. | 本次抽查活动中视力不低于4.8的学生人数占总人数的66.7% | |
| C. | 本次抽查活动中视力不低于4.8学生人数中的极差为300人 | |
| D. | 由活动结果可以知道随着年级的增长,视力低于4.8的人数越来越多,呈上升趋势,那么同年级中抽到视力不低于4.8的学生的概率将越来越小 |
1.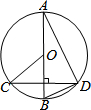 如图所示,AB为⊙O的直径,CD为弦,AB⊥CD,如果∠BOC=50°,那么∠ABD的度数为( )
如图所示,AB为⊙O的直径,CD为弦,AB⊥CD,如果∠BOC=50°,那么∠ABD的度数为( )
 如图所示,AB为⊙O的直径,CD为弦,AB⊥CD,如果∠BOC=50°,那么∠ABD的度数为( )
如图所示,AB为⊙O的直径,CD为弦,AB⊥CD,如果∠BOC=50°,那么∠ABD的度数为( )| A. | 25° | B. | 20° | C. | 65° | D. | 50° |
18.下列代数式中,次数为4的单项式是( )
| A. | x4+y4 | B. | xy2 | C. | 4xy | D. | x3y |
2.-2-2的倒数等于( )
| A. | -4 | B. | 4 | C. | -$\frac{1}{4}$ | D. | $\frac{1}{4}$ |
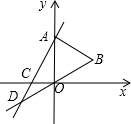 如图,点A的坐标为(0,2$\sqrt{3}$),△AOB是等边三角形,AC⊥AB,直线AC与x轴和直线OB分别相交于点C和点D,双曲线y=$\frac{k}{x}$经过点B.
如图,点A的坐标为(0,2$\sqrt{3}$),△AOB是等边三角形,AC⊥AB,直线AC与x轴和直线OB分别相交于点C和点D,双曲线y=$\frac{k}{x}$经过点B.