题目内容
4.若二次函数y=x2+bx的图象的对称轴是直线x=2,则关于x的方程x2+bx=5的解为( )| A. | x1=0,x2=4 | B. | x1=1,x2=5 | C. | x1=1,x2=-5 | D. | x1=-1,x2=5 |
分析 根据题意可知抛物线经过点(0,0),由抛物线的对称性可求得b=-4,然后将b=-4代入方程得到关于x的一元二次方程,最后的方程的解即可.
解答 解:令y=0得:x2+bx=0.
解得:x1=0,x2=-b.
∵抛物线的对称轴为x=2,
∴-b=4.
解得:b=-4.
将b=-4代入x2+bx=5得:x2-4x=5.
整理得:x2-4x-5=0,即(x-5)(x+1)=0.
解得:x1=5,x2=-1.
故选:D.
点评 本题主要考查的是抛物线与x轴的交点,利用抛物线的对称性求得b的值是解题的关键.

练习册系列答案
相关题目
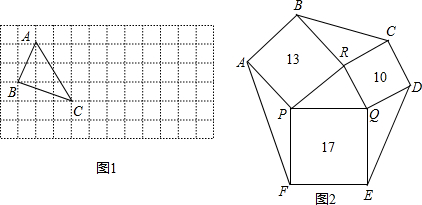
 某城市有座古塔,现要实际测量这座古塔外墙底部的底角(图中∠ABC)的大小,请运用你所学的知识设计出测量方案,并说明理由.
某城市有座古塔,现要实际测量这座古塔外墙底部的底角(图中∠ABC)的大小,请运用你所学的知识设计出测量方案,并说明理由.
 如图是某同学在抛掷图钉的试验中得到的图钉针尖朝上的折线统计图,请估计图钉针尖朝上的概率.
如图是某同学在抛掷图钉的试验中得到的图钉针尖朝上的折线统计图,请估计图钉针尖朝上的概率.