题目内容
9.如图所示,已知线段AB∥CD,AD与BC相交于点K,BE平分∠ABC交AD于点E,BE的延长线交DC的延长线于点P.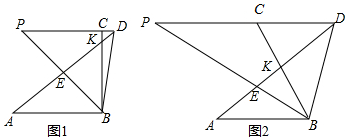
(1)如图1所示,若点E恰好为AD的中点,直接写出线段AB、BC、CD之间的数量关系,不必证明;
(2)如图2所示,若$\frac{AE}{AD}$=$\frac{1}{3}$,猜想线段AB、BC、CD之间的数量关系并证明;
(3)若$\frac{AE}{AD}$=$\frac{1}{n}$,请直接写出线段AB、BC、CD之间的数量关系,不必证明.
分析 (1)AB=BC+CD;由平行线的性质和角平分线的定义得出∠P=∠CBP,证出PC=BC,AE=DE,由AAS证明△ABE≌△DPE,得出对应边相等AB=DP,即可得出结论;
(2)同(1)得:PC=BC,由平行线得出△ABE∽△DPE,得出对应边成比例,得出AB=$\frac{1}{2}$DP=$\frac{1}{2}$(PC+CD),即可得出结论;
(3)同(2),即可得出结论.
解答 解:(1)AB=BC+CD;理由如下:
∵AB∥CD,
∴∠P=∠ABP,
∵BE平分∠ABC,
∴∠ABP=∠CBP,
∴∠P=∠CBP,
∴PC=BC,
∵点E恰好为AD的中点,
∴AE=DE,
在△ABE和△DPE中,$\left\{\begin{array}{l}{∠ABC=∠P}&{\;}\\{∠AEB=∠DEP}&{\;}\\{AE=DE}&{\;}\end{array}\right.$,
∴△ABE≌△DPE(AAS),
∴AB=DP,
∵DP=PC+CD,PC=BC,
∴AB=BC+CD;
(2)AB=$\frac{1}{2}$(BC+CD);理由如下:
同(1)得:PC=BC,
∵$\frac{AE}{AD}$=$\frac{1}{3}$,
∴$\frac{AE}{DE}=\frac{1}{2}$,
∵AB∥CD,
∴△ABE∽△DPE,
∴$\frac{AB}{DP}=\frac{AE}{DE}=\frac{1}{2}$,
∴AB=$\frac{1}{2}$DP=$\frac{1}{2}$(PC+CD),
∵PC=BC,
∴AB=$\frac{1}{2}$(BC+CD);
(3)AB=$\frac{1}{n-1}$(BC+CD);理由如下:
∵$\frac{AE}{AD}$=$\frac{1}{n}$,
∴$\frac{AE}{DE}=\frac{1}{n-1}$,
同(1)得:PC=BC,△ABE∽△DFE,
∴$\frac{AB}{DP}=\frac{AE}{DE}$=$\frac{1}{n-1}$,
∴AB=$\frac{1}{n-1}$(BC+CD).
点评 本题是相似形综合题目,考查了平行线的性质、全等三角形的判定与性质、等腰三角形的判定、相似三角形的判定与性质、比例的性质等知识;本题综合性强,难度较大,需要证明三角形全等或三角形相似才能得出结论.

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案| A. | x1=0,x2=4 | B. | x1=1,x2=5 | C. | x1=1,x2=-5 | D. | x1=-1,x2=5 |
| A. | 16 | B. | 8a | C. | (16+4a) | D. | (16+8a) |
| 月用电量(度) | 25 | 30 | 40 | 50 | 60 |
| 户数 | 1 | 2 | 4 | 2 | 1 |
| A. | 极差是3 | B. | 众数是4 | C. | 中位数40 | D. | 平均数是20.5 |