题目内容
18.请你观察下列各式,用含自然数n(n≧1)的代数式填空,并在表格右侧说明你的理由?| $\sqrt{1+\frac{1}{3}}$=2$\sqrt{\frac{1}{3}}$ | 理由: |
| $\sqrt{2+\frac{1}{4}}$=3$\sqrt{\frac{1}{4}}$ | |
| $\sqrt{3+\frac{1}{5}}$=4$\sqrt{\frac{1}{5}}$ | |
| … | |
| $\sqrt{n+\frac{1}{n+2}}$=(n+1)$\sqrt{\frac{1}{n+2}}$ |
分析 先求得n+$\frac{1}{n+2}$的和,然后再利用完全平方公式将分子进行变形,最后在开方即可.
解答 解:$\sqrt{n+\frac{1}{n+2}}=\sqrt{\frac{n(n+2+1)}{n+2}}$=$\sqrt{\frac{{n}^{2}+2n+1}{n+2}}$=$\sqrt{\frac{(n+1)^{2}}{n+2}}$=(n+1)$\sqrt{\frac{1}{n+2}}$.
故答案为:(n+1)$\sqrt{\frac{1}{n+2}}$.
点评 本题主要考查的是完全平方公式的应用,掌握完全平方公式是解题的关键.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
3.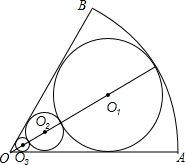 如图所示,扇形AOB中,∠AOB=60°,AO=R,圆O1与AO,BO和弧AB都相切;圆O2和圆O1,AO,BO都相切;圆O3和圆O2;AO,BO都相切;则圆O3的面积为( )
如图所示,扇形AOB中,∠AOB=60°,AO=R,圆O1与AO,BO和弧AB都相切;圆O2和圆O1,AO,BO都相切;圆O3和圆O2;AO,BO都相切;则圆O3的面积为( )
 如图所示,扇形AOB中,∠AOB=60°,AO=R,圆O1与AO,BO和弧AB都相切;圆O2和圆O1,AO,BO都相切;圆O3和圆O2;AO,BO都相切;则圆O3的面积为( )
如图所示,扇形AOB中,∠AOB=60°,AO=R,圆O1与AO,BO和弧AB都相切;圆O2和圆O1,AO,BO都相切;圆O3和圆O2;AO,BO都相切;则圆O3的面积为( )| A. | $\frac{π{R}^{2}}{2187}$ | B. | $\frac{8π{R}^{2}}{2187}$ | C. | $\frac{π{R}^{2}}{729}$ | D. | $\frac{8π{R}^{2}}{729}$ |
 阅读下列材料,并回答问题.
阅读下列材料,并回答问题. 如图,△ABC中,DE垂直平分AC交AB于E,∠A=20°,∠ACB=80°,则∠BCE=60°.
如图,△ABC中,DE垂直平分AC交AB于E,∠A=20°,∠ACB=80°,则∠BCE=60°. 如图,△ABC中,∠C=90°,∠A=30°,BC=1.5cm,则AB的长是3cm.
如图,△ABC中,∠C=90°,∠A=30°,BC=1.5cm,则AB的长是3cm.